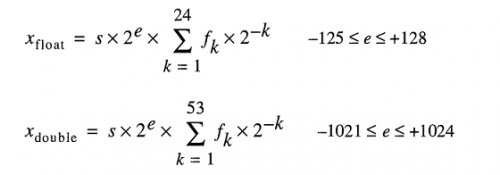Perspektywa projektanta sprzętu

Uważam, że powinienem dodać do tego perspektywę projektanta sprzętu, ponieważ projektuję i buduję sprzęt zmiennoprzecinkowy. Znajomość pochodzenia błędu może pomóc w zrozumieniu tego, co dzieje się w oprogramowaniu, a ostatecznie mam nadzieję, że pomoże to wyjaśnić powody, dla których błędy zmiennoprzecinkowe zdarzają się i wydają się kumulować w czasie.

1. Przegląd

Z inżynieryjnego punktu widzenia, większość operacji zmiennoprzecinkowych będzie miał pewien element błędu, ponieważ sprzęt, który wykonuje obliczenia zmiennoprzecinkowe, musi mieć błąd mniejszy niż połowa jednej jednostki na ostatnim miejscu. W związku z tym wiele urządzeń zatrzyma się przy precyzji, która jest niezbędna tylko do uzyskania Błędu mniej niż połowa jednej jednostki w ostatnim miejscu dla pojedynczej operacji, co jest szczególnie problematyczne w dzieleniu zmiennoprzecinkowym. To, co stanowi pojedynczą operację, zależy od tego, ile operandów Jednostka bierze. Dla większości jest to dwa, ale niektóre jednostki przyjmują 3 lub więcej operandów. Z tego powodu nie ma gwarancji, że powtarzające się operacje spowodują pożądany błąd, ponieważ błędy sumują się w czasie.

2. Standardy

Większość procesorów stosuje standard IEEE-754, ale niektóre używają denormalizowanych lub innych standardów . Na przykład w IEEE-754 istnieje tryb denormalizowany, który umożliwia reprezentację bardzo małych liczb zmiennoprzecinkowych kosztem precyzji. Na następnie jednak obejmie znormalizowany tryb IEEE-754, który jest typowym trybem pracy.

W standardzie IEEE-754 projektanci sprzętu mogą mieć dowolną wartość error / epsilon, o ile jest ona mniejsza niż połowa jednej jednostki na ostatnim miejscu, a wynik musi być mniejszy niż połowa jednej jednostki na ostatnim miejscu dla jednej operacji. To wyjaśnia, dlaczego w przypadku powtarzających się operacji błędy sumują się. Dla podwójnej precyzji IEEE-754 jest to 54 bit, ponieważ 53 bity są używane do reprezentowania części numerycznej (znormalizowanej), zwanej również mantissa, liczby zmiennoprzecinkowej (np. 5.3 in 5.3e5). Kolejne sekcje szczegółowo opisują Przyczyny błędów sprzętowych w różnych operacjach zmiennoprzecinkowych.

3. Przyczyna błędu zaokrąglania w podziale

Główną przyczyną błędu w dzieleniu zmiennoprzecinkowym są algorytmy podziału używane do obliczania ilorazu. Większość systemów komputerowych oblicza podział za pomocą mnożenia przez odwrotnie, głównie w Z=X/Y, Z = X * (1/Y). Podział jest obliczany iteracyjnie, tzn. każdy cykl oblicza kilka bitów ilorazu, aż do osiągnięcia pożądanej precyzji, która dla IEEE-754 jest czymś z błędem mniejszym niż jedna jednostka na ostatnim miejscu. Tabela odwrotności y (1 / Y) jest znana jako ilorazowa tabela wyboru (QST) w wolnym podziale, a rozmiar w bitach ilorazowej tabeli wyboru jest zwykle szerokością radixa lub liczbą bitów ilorazu obliczonego w każdym z nich iteracja, plus kilka bitów ochronnych. Dla standardu IEEE-754, Podwójna precyzja (64-bit), byłaby to wielkość radix dzielnika, plus kilka bitów ochronnych k, gdzie k>=2. Na przykład, typowa tabela wyboru ilorazu dla dzielnika, który oblicza 2 bity ilorazu na raz (radix 4), to 2+2= 4 bity (plus kilka opcjonalnych bitów).

3.1 błąd zaokrąglania podziału: przybliżenie odwrotności

To, jakie są wzajemności w tabeli wyboru ilorazów, zależy w metodzie podziału : powolny podział, taki jak SRT division, lub szybki podział, taki jak Goldschmidt division; każdy wpis jest modyfikowany zgodnie z algorytmem podziału w celu uzyskania najniższego możliwego błędu. W każdym razie, wszystkie wzajemności są przybliżeniami rzeczywistego wzajemności i wprowadzają pewien element błędu. Zarówno metody powolnego dzielenia, jak i szybkiego dzielenia obliczają iloraz iteracyjnie, tzn. oblicza się pewną liczbę bitów ilorazu każdy krok, a następnie wynik jest odejmowany od dywidendy, a dzielnik powtarza kroki, aż błąd będzie mniejszy niż połowa jednej jednostki na ostatnim miejscu. Metody powolnego dzielenia obliczają stałą liczbę cyfr ilorazu w każdym kroku i są zwykle tańsze do zbudowania, a metody szybkiego dzielenia obliczają zmienną liczbę cyfr na krok i są zwykle droższe do zbudowania. Najważniejszą częścią metod podziału jest to, że większość z nich opiera się na powtarzających się mnożenie przez przybliżenie odwrotności, więc są podatne na błędy.

4. Błędy zaokrąglania w innych operacjach: Truncation

5. Operacje Powtarzane

Ponieważ sprzęt wykonujący obliczenia zmiennoprzecinkowe musi tylko dać wynik z błędem mniejszym niż połowa jednej jednostki w ostatnim miejscu dla pojedynczej operacji, błąd będzie rosnąć w stosunku do powtarzających się operacje, jeśli nie są obserwowane. Jest to powód, dla którego w obliczeniach, które wymagają błędu ograniczonego, matematycy używają metod takich jak użycie okrągłej do najbliższej parzystej cyfry w ostatnim miejscu IEEE-754, ponieważ z czasem błędy są bardziej prawdopodobne, aby się wzajemnie anulować, i arytmetyka interwałowaw połączeniu z wariacjami IEEE 754 tryby zaokrąglania do przewidywania błędów zaokrąglania i ich korygowania. Ze względu na niski błąd względny w porównaniu z innymi zaokrągleniami tryb zaokrąglania do najbliższej parzystej cyfry (na ostatnim miejscu) jest domyślnym trybem zaokrąglania IEEE-754.

Należy zauważyć, że domyślny tryb zaokrąglania, zaokrąglanie do najbliższej parzystej cyfry w ostatnim miejscu, gwarantuje błąd mniejszy niż połowa jednej jednostki w ostatnim miejscu dla jednej operacji. Użycie samych okrojenia, zaokrąglenia w górę i zaokrąglenia w dół może spowodować błąd, który jest większy niż połowa jednej jednostki na ostatnim miejscu, ale mniejszy niż jedna jednostka na ostatnim miejscu, więc te tryby nie są zalecane, chyba że są one używane w arytmetyce interwałowej.

6. Podsumowanie

Krótko mówiąc, podstawową przyczyną błędów w operacjach zmiennoprzecinkowych jest połączenie obcinania w sprzęcie i obcinania wzajemności w przypadku dzielenia. Ponieważ standard IEEE-754 wymaga tylko Błędu mniej niż połowa jednej jednostki w ostatnim miejscu dla pojedynczej operacji, błędy zmiennoprzecinkowe nad powtarzającymi się operacjami będą sumować się, chyba że zostaną poprawione.

Kiedy się nawrócisz .1 lub 1/10 do Bazy 2 (binary) otrzymujemy powtarzający się wzór po przecinku, podobnie jak próba reprezentowania 1/3 w bazie 10. Wartość nie jest dokładna, dlatego nie można wykonać dokładnej matematyki za pomocą zwykłych metod zmiennoprzecinkowych.

Większość odpowiedzi tutaj odnosi się do tego pytania w bardzo suchych, technicznych terminach. Chciałbym odnieść się do tego w kategoriach, które normalny człowiek może zrozumieć.

Wyobraź sobie, że próbujesz kroić pizze. Masz zrobotyzowany przecinak do pizzy, który może ciąć plastry pizzy dokładnie na pół. Może zmniejszyć o połowę całą pizzę, lub może zmniejszyć o połowę istniejący kawałek, ale w każdym razie, połowa jest zawsze dokładna.

Ten przecinak do pizzy ma bardzo drobne ruchy, a jeśli zaczniesz od całego pizzy, a następnie zmniejszyć o połowę i kontynuować połowę najmniejszego kawałka za każdym razem, można zrobić połowę 53 razy zanim kawałek będzie zbyt mały, nawet dla jego zdolności wysokiej precyzji. W tym momencie nie możesz już zmniejszyć o połowę tego bardzo cienkiego plasterka, ale musisz go uwzględnić lub wykluczyć w takim stanie, w jakim jest.

Teraz, jak można podzielić wszystkie plastry w taki sposób, że można dodać do jednej dziesiątej (0,1) lub jedną piątą (0,2) pizzy? Zastanów się nad tym i spróbuj to rozpracować. Można nawet spróbować użyć prawdziwa pizza, jeśli masz pod ręką mityczny precyzyjny przecinak do pizzy. :-)

Większość doświadczonych programistów, oczywiście, zna prawdziwą odpowiedź, która jest taka, że nie ma sposobu, aby poskładać dokładnie dziesiątą lub piątą pizzę za pomocą tych plastrów, bez względu na to, jak drobno je pokroić. Możesz zrobić całkiem dobre przybliżenie, a jeśli dodasz przybliżenie 0.1 z przybliżeniem 0.2, otrzymasz całkiem dobre przybliżenie 0.3, ale nadal jest to po prostu, że / align = "left" /

Dla liczb o podwójnej precyzji (co jest precyzją, która pozwala na zmniejszenie o połowę Twojej pizzy 53 razy), liczby od razu mniejsze i większe niż 0,1 to 0,099999999999999999167332731531132594682276248931884765625 i 0.100000000000000055511151231257827021181583404541015625. Ten ostatni jest nieco bliżej 0.1 niż ten pierwszy, więc Parser liczbowy, biorąc pod uwagę wejście 0.1, będzie faworyzował ten drugi.

(różnica między tymi dwoma liczbami jest " najmniejsza slice" , które musimy zdecydować się albo włączyć, co wprowadza odchylenie w górę, lub wykluczyć, co wprowadza odchylenie w dół. Termin techniczny dla tego najmniejszego kawałka to ulp.)

W przypadku 0,2 liczby są takie same, po prostu skalowane przez współczynnik 2. Ponownie faworyzujemy wartość nieco wyższą niż 0,2.

Zauważ, że w obu przypadkach przybliżenia dla 0,1 i 0,2 mają nieznaczne odchylenie w górę. Jeśli dodamy wystarczająco dużo tych uprzedzeń, będą naciskać liczba dalej i dalej od tego, czego chcemy, a w rzeczywistości, w przypadku 0.1 + 0.2, błąd jest na tyle wysoki, że liczba wynikowa nie jest już najbliższą liczbą 0.3.

W szczególności 0.1 + 0.2 to naprawdę 0.1000000000000055511151231257827021181583404541015625 + 0.20000000000000000011102230246251565404236316680908203125 = 0.3000000000000000444089209850062616169452667236328125, natomiast liczba najbliższa 0.3 to faktycznie 0.299999999999999988897769753748434595763683319091796875.

P. S. niektóre języki programowania oferują również przecinarki do pizzy, które potrafią podzielić plastry na dokładne dziesiąte. Chociaż takie przecinarki do pizzy są rzadkie, jeśli masz do nich dostęp, powinieneś go używać, gdy ważne jest, aby móc uzyskać dokładnie jedną dziesiątą lub jedną piątą kawałka.

(Originally posted on Quora.)

Błędy zaokrąglania zmiennoprzecinkowego. 0,1 nie może być tak dokładnie odwzorowane w bazie-2 jak w bazie-10 z powodu braku czynnika pierwszego wynoszącego 5. Podobnie jak 1/3 przyjmuje nieskończoną liczbę cyfr do reprezentowania w dziesiętnym, ale jest "0.1" w bazie-3, 0.1 przyjmuje nieskończoną liczbę cyfr w bazie-2, gdzie nie ma w bazie-10. A komputery nie mają nieskończonej ilości pamięci.

Oprócz innych poprawnych odpowiedzi warto rozważyć skalowanie wartości, aby uniknąć problemów z arytmetyką zmiennoprzecinkową.

Na przykład:

var result = 1.0 + 2.0;     // result === 3.0 returns true

... zamiast:

var result = 0.1 + 0.2;     // result === 0.3 returns false

Wyrażenie 0.1 + 0.2 === 0.3 zwraca false w JavaScript, ale na szczęście arytmetyka liczb całkowitych w zmiennoprzecinkowych jest dokładna, więc błędów reprezentacji dziesiętnej można uniknąć poprzez skalowanie.

Jako praktyczny przykład, aby uniknąć problemów zmiennoprzecinkowych, w których dokładność jest najważniejsza, jest Zalecane¹ do obsługi pieniędzy jako liczba całkowita reprezentująca liczbę centów: 2550 centów zamiast 25.50 dolarów.

¹ Douglas Crockford: JavaScript: the Good Parts : Appendix A - Awful Parts (page 105) .

moja odpowiedź jest dość długa, więc podzieliłem ją na trzy części. Ponieważ pytanie dotyczy matematyki zmiennoprzecinkowej, położyłem nacisk na to, co maszyna faktycznie robi. Zrobiłem to również specyficzne dla podwójnej (64-bitowej) precyzji, ale argument odnosi się w równym stopniu do dowolnej arytmetyki zmiennoprzecinkowej.

Preambuła

An IEEE 754 double-precision binary floating-point format (binary64) liczba reprezentuje liczbę formularz

Value = (-1)^s *(1.na₅₁na₅₀...na₂na₁na₀)₂ * 2^e-1023

W 64 bitach:

• pierwszy bit to bit znaku : 1 jeśli liczba jest ujemna, 0 w przeciwnym razie¹.
• następne 11 bitów to wykładnik, który jest przesunięciem o 1023. Innymi słowy, po odczytaniu bitów wykładnika z liczby podwójnej precyzji, 1023 musi być odejmowany, aby uzyskać moc dwóch.
• Pozostałe 52 bity to significand (lub mantissa). W mantissie "implikowane" 1. jest zawsze² pominięte, ponieważ najbardziej znaczącym bitem dowolnej wartości binarnej jest 1.

¹ - IEEE 754 pozwala na koncepcję podpisanego zera - +0 i -0 są traktowane inaczej: 1 / (+0) jest dodatnią nieskończonością; 1 / (-0) jest ujemną nieskończonością. Dla wartości zerowych mantysa i wykładnik wszystkie bity są zerowe. Uwaga: wartości zerowe (+0 i -0) nie są jawnie klasyfikowane jako denormalne².

² - nie jest tak w przypadku liczb denormalnych , które mają wykładnik przesunięcia równy zero (i implikowany 0.). Zakres denormalnych liczb podwójnej precyzji wynosi d_min ≤ |x / ≤ d_max , gdzie D_min (najmniejsza reprezentowalna liczba niezerowa) wynosi 2^{-1023 - 51} (≈ 4.94 * 10^-324) I d _max (the największa liczba denormalna, dla której mantysa składa się w całości z 1 s) wynosi 2^{-1023 + 1} - 2^{-1023 - 51} (≈ 2.225 * 10^-308).

Zamiana liczby podwójnej precyzji na binarną

Istnieje wiele konwerterów internetowych do konwersji liczby zmiennoprzecinkowej podwójnej precyzji na binarną(np. binaryconvert.com ), ale oto przykładowy kod C#, aby uzyskać reprezentację IEEE 754 dla liczby podwójnej precyzji (oddzielam trzy części z dwukropkami (:):

public static string BinaryRepresentation(double value)
{
    long valueInLongType = BitConverter.DoubleToInt64Bits(value);
    string bits = Convert.ToString(valueInLongType, 2);
    string leadingZeros = new string('0', 64 - bits.Length);
    string binaryRepresentation = leadingZeros + bits;

    string sign = binaryRepresentation[0].ToString();
    string exponent = binaryRepresentation.Substring(1, 11);
    string mantissa = binaryRepresentation.Substring(12);

    return string.Format("{0}:{1}:{2}", sign, exponent, mantissa);
}

Przejdźmy do sedna: pierwotne pytanie

(przejdź do dołu dla wersji TL; DR)

Cato Johnston (pytający) zapytał dlaczego 0.1 + 0.2 != 0.3.

0.1 => 0:01111111011:1001100110011001100110011001100110011001100110011010
0.2 => 0:01111111100:1001100110011001100110011001100110011001100110011010

Zauważ, że mantissa składa się z powtarzających się cyfr 0011. To jest klucz z powodu błędu w obliczeniach-0.1, 0.2 i 0.3 nie mogą być przedstawione w postaci binarnej dokładnie W skończonej Liczba bitów binarnych większa niż 1/9, 1/3 lub 1/7 może być przedstawiona dokładnie w postaci cyfr dziesiętnych.

0.1 = 2^-4 * [1].1001100110011001100110011001100110011001100110011010
0.2 = 2^-3 * [1].1001100110011001100110011001100110011001100110011010

Aby dodać dwie liczby, wykładnik musi być taki sam, tj.:

0.1 = 2^-3 *  0.1100110011001100110011001100110011001100110011001101(0)
0.2 = 2^-3 *  1.1001100110011001100110011001100110011001100110011010
sum = 2^-3 * 10.0110011001100110011001100110011001100110011001100111

Ponieważ suma nie ma formy 2 ⁿ * 1.{BBB} zwiększamy wykładnik o jeden i przesuwamy punkt dziesiętny (binarny ), aby otrzymać:

sum = 2^-2 * 1.0011001100110011001100110011001100110011001100110011(1)

W mantysie są teraz 53 bity(53. jest w nawiasach kwadratowych w linii powyżej). Domyślnie tryb zaokrąglania dla IEEE 754 to "Round to Nearest " - tzn. jeśli liczba x mieści się pomiędzy dwiema wartościami a i b , wartość, w której najmniej znaczący wybierany jest bit równy zero.

a = 2^-2 * 1.0011001100110011001100110011001100110011001100110011
x = 2^-2 * 1.0011001100110011001100110011001100110011001100110011(1)
b = 2^-2 * 1.0011001100110011001100110011001100110011001100110100

Zauważ, że a i b różnią się tylko ostatnim bitem; ...0011 + 1 = ...0100. W tym przypadku wartość z najmniej znaczącym bitem zera wynosi b , więc suma wynosi:

sum = 2^-2 * 1.0011001100110011001100110011001100110011001100110100

TL; DR

Zapisanie 0.1 + 0.2 w reprezentacji binarnej IEEE 754 (z dwukropkami oddzielającymi trzy części) i porównanie go z 0.3, jest to (umieściłem różne bity w nawiasach kwadratowych):

0.1 + 0.2 => 0:01111111101:0011001100110011001100110011001100110011001100110[100]
0.3       => 0:01111111101:0011001100110011001100110011001100110011001100110[011]

Wartości dziesiętne to:

0.1 + 0.2 => 0.300000000000000044408920985006...
0.3       => 0.299999999999999988897769753748...

Różnica jest dokładnie 2^-54, czyli ~5.5511151231258 × 10^-17 - nieistotne (dla wielu aplikacji) w porównaniu z oryginalnymi wartościami.

Porównywanie ostatnich kilku bitów liczby zmiennoprzecinkowej jest z natury niebezpieczne, ponieważ każdy, kto czyta słynne " to, co każdy informatyk powinien wiedzieć o arytmetyce zmiennoprzecinkowej " (która obejmuje wszystkie główne części tej odpowiedzi), wiedzieć.

Większość kalkulatorów używa dodatkowych wartych cyfr , aby obejść ten problem, czyli jak 0.1 + 0.2 da 0.3: kilka ostatnich bitów jest zaokrąglonych.

Liczby zmiennoprzecinkowe przechowywane w komputerze składają się z dwóch części, liczby całkowitej i wykładnika, na które baza jest pobierana i mnożona przez część całkowitą.

Gdyby komputer działał w bazie 10, 0.1 byłby 1 x 10⁻¹, 0.2 będzie 2 x 10⁻¹, A 0.3 będzie 3 x 10⁻¹. Matematyka całkowita jest łatwa i dokładna, więc dodanie 0.1 + 0.2 oczywiście spowoduje 0.3.

Problem dotyczy liczb, które można przedstawić dokładnie w bazie 10, ale nie w bazie 2. Liczby te należy zaokrąglić do ich najbliższego odpowiednika. Przy założeniu bardzo popularnego 64-bitowego formatu zmiennoprzecinkowego IEEE najbliższą liczbą 0.1 jest 3602879701896397 x 2⁻⁵⁵, a najbliższą liczbą 0.2 jest 7205759403792794 x 2⁻⁵⁵; dodanie ich razem daje 10808639105689191 x 2⁻⁵⁵ lub dokładną wartość dziesiętną 0.3000000000000000444089209850062616169452667236328125. Floating liczby punktów są zazwyczaj zaokrąglane do wyświetlania.

Zmiennoprzecinkowy błąd zaokrąglania. Z Co Każdy Informatyk Powinien Wiedzieć O Arytmetyce Zmiennoprzecinkowej :

Wyciskanie nieskończenie wielu liczb rzeczywistych do skończonej liczby bitów wymaga przybliżonej reprezentacji. Chociaż istnieje nieskończenie wiele liczb całkowitych, w większości programów wynik obliczeń całkowitych może być przechowywany w 32 bitach. Natomiast, biorąc pod uwagę dowolną stałą liczbę bitów, większość obliczeń z liczbami rzeczywistymi wytworzy ilości, które nie mogą być dokładnie reprezentowane za pomocą wielu bitów. W związku z tym wynik obliczeń zmiennoprzecinkowych musi być często zaokrąglany, aby dopasować się z powrotem do jego skończonej reprezentacji. Ten błąd zaokrąglania jest charakterystyczną cechą obliczeń zmiennoprzecinkowych.

Moje obejście:

function add(a, b, precision) {
    var x = Math.pow(10, precision || 2);
    return (Math.round(a * x) + Math.round(b * x)) / x;
}

precision odnosi się do liczby cyfr, które chcesz zachować po przecinku podczas dodawania.

Opublikowano wiele dobrych odpowiedzi, ale chciałbym dodać jeszcze jedną.

Nie wszystkie liczby mogą być reprezentowane przez / doubles Na przykład liczba "0.2" będzie reprezentowana jako "0.200000003" w pojedynczej precyzji w standardzie IEEE754 punktu zmiennoprzecinkowego.

Model zapisywania liczb rzeczywistych pod maską przedstawia liczby float jako

Mimo, że możesz łatwo wpisać 0.2, FLT_RADIX i DBL_RADIX jest 2, a nie 10 dla komputera z FPU, który używa " standardu IEEE dla binarnej arytmetyki zmiennoprzecinkowej (ISO / IEEE Std 754-1985)".

Niektóre statystyki związane z tym słynnym pytaniem o podwójną precyzję.

Przy dodawaniu wszystkich wartości (a + b) za pomocą kroku 0.1 (od 0.1 do 100) mamy ~15% szans błędu dokładności . Zauważ, że błąd może spowodować nieco większe lub mniejsze wartości. Oto kilka przykładów:

0.1 + 0.2 = 0.30000000000000004 (BIGGER)
0.1 + 0.7 = 0.7999999999999999 (SMALLER)
...
1.7 + 1.9 = 3.5999999999999996 (SMALLER)
1.7 + 2.2 = 3.9000000000000004 (BIGGER)
...
3.2 + 3.6 = 6.800000000000001 (BIGGER)
3.2 + 4.4 = 7.6000000000000005 (BIGGER)

Po odjęciu wszystkich wartości (a-b Gdzie A > b) przy użyciu kroku 0,1 (od 100 do 0,1) mamy ~34% szans błędu dokładności. Oto kilka przykłady:

0.6 - 0.2 = 0.39999999999999997 (SMALLER)
0.5 - 0.4 = 0.09999999999999998 (SMALLER)
...
2.1 - 0.2 = 1.9000000000000001 (BIGGER)
2.0 - 1.9 = 0.10000000000000009 (BIGGER)
...
100 - 99.9 = 0.09999999999999432 (SMALLER)
100 - 99.8 = 0.20000000000000284 (BIGGER)

*15% i 34% są naprawdę ogromne, więc Zawsze używaj BigDecimal, gdy precyzja ma duże znaczenie. Przy 2 cyfrach dziesiętnych (krok 0.01) sytuacja pogarsza się nieco bardziej (18% i 36%).

Nie, Nie złamane, ale większość ułamków dziesiętnych musi być przybliżona

Podsumowanie

Arytmetyka zmiennoprzecinkowa jest dokładna, niestety, nie pasuje dobrze do naszej zwykłej reprezentacji liczb bazowych 10, więc okazuje się, że często dajemy jej Dane wejściowe, które są nieco odbiegające od tego, co napisaliśmy.

Parzyste liczby proste, takie jak 0.01, 0.02, 0.03, 0.04 ... 0.24 nie są reprezentowalne dokładnie jako ułamki binarne. Jeśli policzysz 0.01, .02, .03 ..., dopiero gdy dojdziesz do 0.25 otrzymasz pierwszą frakcję reprezentowalną w bazie₂. Jeśli spróbujesz tego używając FP, twój 0.01 byłby nieco wyłączony, więc jedyny sposób, aby dodać 25 z nich do ładnego dokładnego 0.25 wymagałby długiego łańcucha przyczynowości obejmującego bity ochronne i zaokrąglenia. Trudno to przewidzieć, więc podnosimy ręce i mówimy "FP jest niedokładne", ale to nie do końca prawda.

Stale dajemy sprzętowi FP coś, co wydaje się proste w bazie 10 ale jest ułamkiem powtarzającym się w bazie 2.

Jak to się stało?

Gdy zapisujemy dziesiętnym, każdy ułamek (konkretnie każdy kończący dziesiętny) jest liczbą wymierną postaci

           a / (2 ⁿ x 5 ^m)

W systemie binarnym otrzymujemy tylko 2ⁿ termin, czyli:

a / 2 ⁿ

Więc w układzie dziesiętnym nie możemy reprezentować ¹/₃. Ponieważ baza 10 zawiera 2 jako czynnik pierwszy, każda liczba, którą możemy zapisać jako ułamek binarny , również może być zapisana jako ułamek bazowy 10. Jednak prawie nic, co piszemy jako podstawę₁₀ ułamek można przedstawić w postaci binarnej. W zakresie od 0,01, 0,02, 0,03 ... 0.99, tylko trzy liczby mogą być reprezentowane w naszym formacie FP: 0.25, 0.50 i 0.75, ponieważ są to liczby 1/4, 1/2 i 3/4, wszystkie liczby z czynnikiem pierwszym, używając tylko liczby 2 ^N term.

W bazie₁₀ nie możemy reprezentować ¹/₃. Ale w binarnych, nie możemy zrobić ¹/₁₀lub ¹/₃.

Tak więc, podczas gdy każdy ułamek binarny może być zapisany w dziesiętnym, odwrotność nie jest prawdziwa. W rzeczywistości większość ułamków dziesiętnych powtarza się w postaci binarnej.

radzenie sobie z tym

Deweloperzy są zwykle poinstruowani, aby zrobić porównania, lepsze Rady może to być zaokrąglenie do wartości całkowych (w bibliotece C: round () i roundf (), tzn. pozostanie w formacie FP), a następnie porównanie. Zaokrąglanie do określonej długości ułamka dziesiętnego rozwiązuje większość problemów z wyjściem.

Ponadto, na rzeczywistych problemach chrupania liczb (problemy, dla których FP został wymyślony na wczesnych, przerażająco drogich komputerach) stałe fizyczne wszechświata i wszystkie inne pomiary są znane tylko stosunkowo niewielkiej liczbie znaczących liczb, więc cały problem kosmos i tak był "niedokładny". "Dokładność" FP nie stanowi problemu w tego typu aplikacjach.

Cały problem pojawia się naprawdę, gdy ludzie próbują używać FP do liczenia fasoli. Działa do tego, ale tylko wtedy, gdy trzymamy się wartości całkowych, co w pewnym sensie podważa sens jej używania. dlatego mamy wszystkie biblioteki oprogramowania ułamków dziesiętnych.

Uwielbiam Pizza Odpowiedz przez Chris , ponieważ opisuje rzeczywisty problem, a nie tylko zwykłe ręczne oszczędzanie o "niedokładność". Gdyby FP były po prostu "niedokładne", moglibyśmy to naprawić i zrobilibyśmy to kilkadziesiąt lat temu. Powodem, dla którego nie mamy, jest to, że format FP jest kompaktowy i szybki i jest to najlepszy sposób na schrupanie wielu liczb. Jest to również dziedzictwo z epoki kosmicznej i wyścigu zbrojeń oraz wczesne próby rozwiązania dużych problemów z bardzo powolnymi komputerami wykorzystującymi małe systemy pamięci. (Czasami pojedynczerdzenie magnetyczne do 1-bitowego przechowywania, ale to jest inna historia.)

Podsumowanie

Jeśli tylko liczysz fasolę w banku, rozwiązania programowe, które wykorzystują reprezentacje dziesiętne, działają doskonale. Ale nie można w ten sposób uprawiać chromodynamiki kwantowej ani aerodynamiki.

Próbowałeś taśmy klejącej?

Spróbuj określić, kiedy występują błędy i naprawić je krótkimi instrukcjami if, nie jest to ładne, ale w przypadku niektórych problemów jest to jedyne rozwiązanie i jest to jedno z nich.

 if( (n * 0.1) < 100.0 ) { return n * 0.1 - 0.000000000000001 ;}
                    else { return n * 0.1 + 0.000000000000001 ;}    

Miałem ten sam problem w projekcie symulacji naukowej w c#, i mogę ci powiedzieć, że jeśli zignorujesz Efekt motyla, to zmieni się w wielkiego tłustego smoka i ugryzie cię w a**

Te dziwne liczby pojawiają się, ponieważ komputery używają systemu liczb binarnych (baza 2) do celów obliczeniowych, podczas gdy my używamy dziesiętnych(baza 10).

Istnieje większość liczb ułamkowych, których nie można dokładnie przedstawić ani w binarnym, ani w dziesiętnym, ani w obu. Wynik-zaokrąglona (ale precyzyjna) liczba wyników.

Mogę tylko dodać; ludzie zawsze zakładają, że to jest problem z komputerem, ale jeśli liczysz rękami (baza 10), nie możesz dostać (1/3+1/3=2/3)=true, chyba że masz nieskończoność do dodania 0.333... do 0.333.. podobnie jak w przypadku problemu (1/10+2/10)!==3/10 w bazie 2, obciąć go do 0.333 + 0.333 = 0.666 i prawdopodobnie zaokrąglić go do 0.667, co również byłoby technicznie niedokładne.

Licz w trzech, a trzecie nie stanowią jednak problemu - może jakaś rasa z 15 palcami na każdej ręce zapytałaby, Dlaczego Twój dziesiętny Matematyka została złamana...

Wiele z licznych duplikatów tego pytania Pyta o wpływ zaokrąglania zmiennoprzecinkowego na określone liczby. W praktyce łatwiej jest zorientować się, jak to działa, patrząc na dokładne wyniki obliczeń zainteresowania, a nie tylko czytając o tym. Niektóre języki oferują takie sposoby, jak konwersja float lub double na BigDecimal w Javie.

Ponieważ jest to pytanie językowo-agnostyczne, potrzebne są narzędzia językowo-agnostyczne, takie jak dziesiętne do Konwerter Zmiennoprzecinkowy .

Zastosowanie go do liczb w pytaniu, traktowanych jako podwójne:

0.100000000000055511151231257827021181583404541015625,

0.2000000000000011102230246251565404236316680908203125,

0.39999999999999988897769753748434595763683319091796875 i

Dodanie pierwszego dwie liczby ręcznie lub w kalkulatorze dziesiętnym, takim jak Full Precision Calculator , pokazuje dokładną sumę rzeczywistych wejść wynosi 0.300000000000000000166533453693773481063544750213623046875.

Gdyby zaokrąglono go w dół do ekwiwalentu 0,3, błąd zaokrąglania wynosiłby 0,0000000000000000000000277555756156289135105907917022705078125. Zaokrąglenie do ekwiwalentu 0,3000000000000000004 daje również błąd zaokrąglenia 0,00000000000000000000277555756156289135105907917022705078125. Na stosuje się tie breaker od rundy do parzystej.

Wracając do konwertera zmiennoprzecinkowego, surowy szesnastkowy dla 0,30000000000000000004 to 3fd3333333333334, który kończy się parzystą cyfrą i dlatego jest poprawnym wynikiem.

Biorąc pod uwagę, że nikt o tym nie wspomniał...

Niektóre języki wysokiego poziomu, takie jak Python i Java, mają narzędzia do przezwyciężania binarnych ograniczeń zmiennoprzecinkowych. Na przykład:

• Python 's decimal module i Java' S BigDecimal klasa , która wewnętrznie reprezentuje liczby z notacją dziesiętną (w przeciwieństwie do notacji binarnej). Obie mają ograniczoną precyzję, więc nadal są podatne na błędy, jednak rozwiązują najczęstsze problemy z binarną zmiennoprzecinkową arytmetyka.

  10 centów plus 20 centów to zawsze dokładnie trzydzieści centów:]}

  >>> 0.1 + 0.2 == 0.3
  False
  >>> Decimal('0.1') + Decimal('0.2') == Decimal('0.3')
  True
  

  Moduł Pythona decimal jest oparty na standardzie IEEE 854-1987.

• Python 's fractions module i Apache Common' s BigFraction klasa . Obie reprezentują Liczby wymierne jako pary (numerator, denominator) i mogą dawać dokładniejsze wyniki niż arytmetyka dziesiętna zmiennoprzecinkowa.

Żadne z tych rozwiązań jest doskonała (zwłaszcza jeśli patrzymy na wyniki, lub jeśli wymagamy bardzo wysokiej precyzji), ale mimo to rozwiązuje wiele problemów z binarną arytmetyką zmiennoprzecinkową.

Rodzaj matematyki zmiennoprzecinkowej, która może być zaimplementowana w komputerze cyfrowym, wykorzystuje przybliżenie liczb rzeczywistych i operacje na nich. (Wersja standard obejmuje ponad pięćdziesiąt stron dokumentacji i ma komitet, który zajmie się jej erratą i dalszym udoskonalaniem.)

To przybliżenie jest mieszaniną przybliżeń różnego rodzaju, z których każda może być ignorowana lub starannie rozliczana ze względu na swój specyficzny sposób odchylenia od dokładność. Wiąże się to również z wieloma wyjątkowymi przypadkami zarówno na poziomie sprzętu, jak i oprogramowania, które większość ludzi przechodzi obok, udając, że nie zauważają.

Jeśli potrzebujesz nieskończonej precyzji (używając liczby π, na przykład, zamiast jednej z wielu krótszych podstawek), powinieneś napisać lub użyć symbolicznego programu matematycznego.

Ale jeśli nie masz nic przeciwko temu, że czasami matematyka zmiennoprzecinkowa jest rozmyta w wartości i logice, a błędy mogą szybko się kumulować, i możesz napisać swoje wymagania i testy, aby na to pozwolić, wtedy twój kod może często poradzić sobie z tym, co jest w Twoim FPU.

Dla Zabawy, grałem z reprezentacji pływaków, zgodnie z definicjami ze standardu C99 i napisałem kod poniżej.

Kod drukuje binarną reprezentację pływaków w 3 oddzielonych grupach

SIGN EXPONENT FRACTION

A następnie wypisuje sumę, która po zsumowaniu z wystarczającą precyzją pokaże wartość, która naprawdę istnieje w sprzęcie.

Więc kiedy napiszesz float x = 999..., kompilator przekształci tę liczbę w reprezentację bitową wydrukowaną przez Funkcja xx taka, że suma wydrukowana przez funkcję yy jest równa podanej liczbie.

Po kodzie dołączam sesję konsoli, w której obliczam sumę pojęć dla obu stałych (minus PI i 9999999999), które naprawdę istnieją w sprzęcie, wstawione tam przez kompilator.

#include <stdio.h>
#include <limits.h>

void
xx(float *x)
{
    unsigned char i = sizeof(*x)*CHAR_BIT-1;
    do {
        switch (i) {
        case 31:
             printf("sign:");
             break;
        case 30:
             printf("exponent:");
             break;
        case 23:
             printf("fraction:");
             break;

        }
        char b=(*(unsigned long long*)x&((unsigned long long)1<<i))!=0;
        printf("%d ", b);
    } while (i--);
    printf("\n");
}

void
yy(float a)
{
    int sign=!(*(unsigned long long*)&a&((unsigned long long)1<<31));
    int fraction = ((1<<23)-1)&(*(int*)&a);
    int exponent = (255&((*(int*)&a)>>23))-127;

    printf(sign?"positive" " ( 1+":"negative" " ( 1+");
    unsigned int i = 1<<22;
    unsigned int j = 1;
    do {
        char b=(fraction&i)!=0;
        b&&(printf("1/(%d) %c", 1<<j, (fraction&(i-1))?'+':')' ), 0);
    } while (j++, i>>=1);

    printf("*2^%d", exponent);
    printf("\n");
}

void
main()
{
    float x=-3.14;
    float y=999999999;
    printf("%lu\n", sizeof(x));
    xx(&x);
    xx(&y);
    yy(x);
    yy(y);
}

Tutaj jest sesją konsoli, w której obliczam rzeczywistą wartość float, która istnieje w sprzęcie. Użyłem bc aby wydrukować sumę pojęć wypisanych przez główny program. Można wstawić tę sumę w Pythonie repl lub coś podobnego.

-- .../terra1/stub
@ qemacs f.c
-- .../terra1/stub
@ gcc f.c
-- .../terra1/stub
@ ./a.out
sign:1 exponent:1 0 0 0 0 0 0 fraction:0 1 0 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 1
sign:0 exponent:1 0 0 1 1 1 0 fraction:0 1 1 0 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0
negative ( 1+1/(2) +1/(16) +1/(256) +1/(512) +1/(1024) +1/(2048) +1/(8192) +1/(32768) +1/(65536) +1/(131072) +1/(4194304) +1/(8388608) )*2^1
positive ( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
-- .../terra1/stub
@ bc
scale=15
( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
999999999.999999446351872

To jest to. Wartość 999999999 jest w rzeczywistości

999999999.999999446351872

Możesz również sprawdzić za pomocą bc, że -3,14 również jest zaburzone. Nie zapomnij ustawić współczynnika scale w bc.

Wyświetlana suma jest tym, co wewnątrz sprzętu. Wartość uzyskasz obliczając to zależy od ustawionej skali. Ustawiłem współczynnik scale na 15. Matematycznie, z nieskończoną precyzją, wydaje się, że jest to 1.000.000.000.

Aby zaoferować najlepsze rozwiązanie mogę powiedzieć, że odkryłem następującą metodę:

parseFloat((0.1 + 0.2).toFixed(10)) => Will return 0.3

Wyobraź sobie, że dodasz dwie liczby float, takie jak 0.2 i 0.7 Oto jest: 0.2 + 0.7 = 0.8999999999999999.

Twój oczekiwany wynik był 0.9 to znaczy w tym przypadku potrzebujesz wyniku z 1-cyfrową precyzją. Więc powinieneś użyć (0.2 + 0.7).tofixed(1) ale nie możesz po prostu podać określonego parametru tofixed (), ponieważ zależy on od podanej liczby, na przykład

`0.22 + 0.7 = 0.9199999999999999`

W tym przykładzie potrzebujesz 2 cyfr precyzji, więc powinna być toFixed(2), więc jaki powinien być parametr, aby pasował do każdej podanej liczby float?

Można powiedzieć Niech będzie 10 w każdej sytuacji wtedy:

(0.2 + 0.7).toFixed(10) => Result will be "0.9000000000"

parseFloat((0.2 + 0.7).toFixed(10)) => Result will be 0.9

Teraz, gdy znalazłeś rozwiązanie, lepiej zaoferować je jako funkcję taką jak ta:

function floatify(number){
           return parseFloat((number).toFixed(10));
        }

Spróbujmy sam:

function floatify(number){
       return parseFloat((number).toFixed(10));
    }
 
function addUp(){
  var number1 = +$("#number1").val();
  var number2 = +$("#number2").val();
  var unexpectedResult = number1 + number2;
  var expectedResult = floatify(number1 + number2);
  $("#unexpectedResult").text(unexpectedResult);
  $("#expectedResult").text(expectedResult);
}
addUp();

input{
  width: 50px;
}
#expectedResult{
color: green;
}
#unexpectedResult{
color: red;
}

<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script>
<input id="number1" value="0.2" onclick="addUp()" onkeyup="addUp()"/> +
<input id="number2" value="0.7" onclick="addUp()" onkeyup="addUp()"/> =
<p>Expected Result: <span id="expectedResult"></span></p>
<p>Unexpected Result: <span id="unexpectedResult"></span></p>

Możesz go użyć w ten sposób:

var x = 0.2 + 0.7;
floatify(x);  => Result: 0.9

Ponieważ W3SCHOOLS sugeruje, że istnieje również inne rozwiązanie, możesz mnożyć i dzielić, aby rozwiązać powyższy problem:

var x = (0.2 * 10 + 0.1 * 10) / 10;       // x will be 0.3

Należy pamiętać, że (0.2 + 0.1) * 10 / 10 w ogóle nie będzie działać, chociaż to wygląda tak samo! Wolę pierwsze rozwiązanie, ponieważ mogę je zastosować jako funkcję, która konwertuje pływak wejściowy na dokładny pływak wyjściowy.

Inny sposób na to: używane są 64 bity do reprezentowania liczb. W konsekwencji nie ma możliwości, aby więcej niż 2**64 = 18,446,744,073,709,551,616 różnych liczb można dokładnie przedstawić.

Jednak Matematyka mówi, że istnieje nieskończenie wiele miejsc po przecinku między 0 a 1. IEEE 754 definiuje kodowanie, aby efektywnie używać tych 64 bitów dla znacznie większej przestrzeni liczbowej plus NaN i + / - nieskończoności, więc istnieją luki między dokładnie reprezentowanymi liczbami wypełnionymi tylko liczbami / align = "left" /

Niestety 0.3

Ponieważ ten wątek rozwinął się nieco w ogólną dyskusję nad bieżącymi implementacjami zmiennoprzecinkowymi, dodam, że istnieją projekty naprawiające ich problemy.

Spójrz na https://posithub.org na przykład / , który prezentuje Typ liczby o nazwie posit (i jego poprzednik unum), który obiecuje oferować lepszą dokładność przy mniejszej liczbie bitów. Jeśli moje zrozumienie jest poprawne, to również rozwiązuje tego rodzaju problemy w pytaniu. Dość ciekawy projekt, osoba za nim stojąca jest matematykiem it dr John Gustafson . Całość jest open source, z wieloma rzeczywistymi implementacjami w C / C++, Pythonie, Julii i C # ( https://hastlayer.com/arithmetics).

Matematyka.sum (javascript ) .... rodzaj zamiennika operatora

.1 + .0001 + -.1 --> 0.00010000000000000286
Math.sum(.1 , .0001, -.1) --> 0.0001

Object.defineProperties(Math, {
    sign: {
        value: function (x) {
            return x ? x < 0 ? -1 : 1 : 0;
            }
        },
    precision: {
        value: function (value, precision, type) {
            var v = parseFloat(value), 
                p = Math.max(precision, 0) || 0, 
                t = type || 'round';
            return (Math[t](v * Math.pow(10, p)) / Math.pow(10, p)).toFixed(p);
        }
    },
    scientific_to_num: {  // this is from https://gist.github.com/jiggzson
        value: function (num) {
            //if the number is in scientific notation remove it
            if (/e/i.test(num)) {
                var zero = '0',
                        parts = String(num).toLowerCase().split('e'), //split into coeff and exponent
                        e = parts.pop(), //store the exponential part
                        l = Math.abs(e), //get the number of zeros
                        sign = e / l,
                        coeff_array = parts[0].split('.');
                if (sign === -1) {
                    num = zero + '.' + new Array(l).join(zero) + coeff_array.join('');
                } else {
                    var dec = coeff_array[1];
                    if (dec)
                        l = l - dec.length;
                    num = coeff_array.join('') + new Array(l + 1).join(zero);
                }
            }
            return num;
         }
     }
    get_precision: {
        value: function (number) {
            var arr = Math.scientific_to_num((number + "")).split(".");
            return arr[1] ? arr[1].length : 0;
        }
    },
    diff:{
        value: function(A,B){
            var prec = this.max(this.get_precision(A),this.get_precision(B));
            return +this.precision(A-B,prec);
        }
    },
    sum: {
        value: function () {
            var prec = 0, sum = 0;
            for (var i = 0; i < arguments.length; i++) {
                prec = this.max(prec, this.get_precision(arguments[i]));
                sum += +arguments[i]; // force float to convert strings to number
            }
            return Math.precision(sum, prec);
        }
    }
});

Idea polega na używaniu operatorów matematycznych, aby uniknąć błędów float

Math.diff(0.2, 0.11) == 0.09 // true
0.2 - 0.11 == 0.09 // false

Inne pytanie zostało nazwane jako DUPLIKAT tego:

W C++, dlaczego wynik cout << x różni się od wartości, którą debugger pokazuje dla x?

x w pytaniu jest zmienną float.

Przykładem może być

float x = 9.9F;

Debuger pokazuje 9.89999962, Wyjście operacji cout to 9.9.

Okazuje się, że domyślna precyzja cout dla float wynosi 6, więc zaokrągla się do 6 dziesiętnych cyfry.

Zobacz tutaj dla odniesienia

Sine Python 3.5 możesz użyć funkcji math.isclose() w Warunkach if

import math

if math.isclose(0.1 + 0.2, 0.3, abs_tol=0.01):
    pass

_{to było właściwie zamierzone jako odpowiedź na to pytanie -- które zostało zamknięte jako DUPLIKAT to pytanie , podczas gdy składałem tę odpowiedź, więc teraz nie mogę jej tam umieścić... więc napiszę tutaj!}

Podsumowanie pytania:

Na arkuszu 10^-8/1000 i 10^-11 oceniają jako równe podczas gdy w VBA nie.

W arkuszu kalkulacyjnym, liczby są domyślne do Notacja Naukowa.

Jeśli zmienisz komórki na format liczby (Ctrl+1) Z Number z 15 przecinkami dziesiętnymi otrzymujemy:

=10^-11 returns 0.000000000010000
=10^(-8/1000) returns 0.981747943019984

Tak więc, na pewno nie są takie same... jeden to prawie zero, a drugi tylko około 1.

Excel nie został zaprojektowany do radzenia sobie z ekstremalnie małymi liczbami - przynajmniej nie z instalacją zapasów. Istnieją dodatki, które pomagają poprawić precyzję numerów.

Excel został zaprojektowany w zgodnie ze STANDARDEM IEEE dla binarnej arytmetyki zmiennoprzecinkowej ( IEEE 754 ). Standard określa, w jaki sposób liczby zmiennoprzecinkowe są przechowywane i obliczane. Standard IEEE 754 jest powszechnie stosowany, ponieważ pozwala na przechowywanie liczb zmiennoprzecinkowych w rozsądnej ilości miejsca, a obliczenia mogą następować stosunkowo szybko.

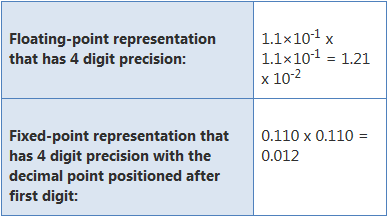
Zaletą reprezentacji zmiennoprzecinkowej jest to, że może obsługiwać szerszy zakres wartości. Na przykład, a reprezentacja fixed-point, która ma 5 cyfr dziesiętnych z punktem dziesiętnym umieszczonym za trzecią cyfrą może reprezentować liczby 123.34, 12.23, 2.45, itd. natomiast reprezentacja zmiennoprzecinkowa z 5-cyfrową precyzją może reprezentować 1.2345, 12345, 0.00012345 itd. Podobnie, reprezentacja zmiennoprzecinkowa umożliwia również obliczenia w szerokim zakresie wielkości przy zachowaniu precyzji. Na przykład,

Inne Bibliografia:

• wsparcie biurowe : Wyświetlanie liczb w notacji naukowej (wykładniczej)
• Microsoft 365 Blog : zrozumienie precyzji zmiennoprzecinkowej , aka " dlaczego Excel daje mi pozornie błędne odpowiedzi?"
• wsparcie biurowe : Ustaw precyzję zaokrąglania w Excelu
• Wsparcie Biurowe : POWER Funkcja
• SuperUser : co to jest największa wartość (liczba), którą mogę zapisać w zmiennej Excel VBA?