Co oznacza "coalgebra" w kontekście programowania?
Kilka razy słyszałem określenie "coalgebras" w programowaniu funkcyjnym i kręgach PLT, zwłaszcza gdy dyskusja dotyczy obiektów, komonad, soczewek itp. Googlowanie tego terminu daje strony, które dają matematyczny opis tych struktur, co jest dla mnie dość niezrozumiałe. Czy ktoś może wyjaśnić, co znaczą coalgebry w kontekście programowania, jakie są ich znaczenie i jak odnoszą się do obiektów i komonad?
4 answers
Algebry
Myślę, że punktem wyjścia byłoby zrozumienie idei algebry . Jest to tylko uogólnienie struktur algebraicznych, takich jak grupy, pierścienie, monoidy i tak dalej. Większość czasu, te rzeczy są wprowadzane w kategoriach zestawów, ale ponieważ jesteśmy wśród przyjaciół, będę mówić o typach Haskell zamiast. (Nie mogę się oprzeć użyciu greckich liter-sprawiają, że wszystko wygląda chłodniej!)
Algebra jest więc tylko typem τ z pewnym funkcje i tożsamości. Funkcje te przyjmują różne liczby argumentów typu τ i wytwarzają τ: uncurried, wszystkie wyglądają jak (τ, τ,…, τ) → τ. Mogą również posiadać "tożsamości" - elementy τ, które mają specjalne zachowanie z niektórymi funkcjami.
τ z funkcją mappend ∷ (τ, τ) → τ i tożsamością mzero ∷ τ. Inne przykłady obejmują rzeczy takie jak grupy (które są podobnie jak monoidy, z wyjątkiem dodatkowych invert ∷ τ → τ funkcja), pierścienie, kraty i tak dalej.
Wszystkie funkcje działają na τ, ale mogą mieć różne właściwości. Możemy je zapisać jako τⁿ → τ, gdzie τⁿ mapy do krotki n τ. W ten sposób sensowne jest myślenie o tożsamości jako τ⁰ → τ, gdzie τ⁰ jest tylko pustą krotką (). Możemy więc teraz uprościć ideę algebry: jest to po prostu jakiś typ z pewną liczbą funkcji.
Algebra jest po prostu powszechnym wzorem w matematyce, który "factored out", tak jak robimy z kodem. Ludzie zauważyli, że cała masa ciekawych rzeczy-wspomniane monoidy, grupy, kraty itp.-wszystkie podążają za podobnym wzorcem, więc to wyabstrahowali. Zaleta tego jest taka sama jak w programowaniu: tworzy dowody wielokrotnego użytku i ułatwia pewne rodzaje rozumowania.
F-Algebry
Nie skończyliśmy jednak z faktoringiem. Do tej pory mamy kilka funkcjiτⁿ → τ. Możemy zrobić sprytny trik, aby połączyć je wszystkie w jedną funkcję. W szczególności przyjrzyjmy się monoidom: mamy mappend ∷ (τ, τ) → τ i mempty ∷ () → τ. Możemy przekształcić je w jedną funkcję używając typu sum - Either. Wyglądałoby to tak:
op ∷ Monoid τ ⇒ Either (τ, τ) () → τ
op (Left (a, b)) = mappend (a, b)
op (Right ()) = mempty
Możemy użyć tej transformacji wielokrotnie, aby połączyć wszystkie funkcje τⁿ → τw jedną jedynkę, dla dowolnej algebry. (W rzeczywistości możemy to zrobić dla dowolnej liczby funkcji a → τ, b → τ i tak dalej dla dowolnych a, b,….)
To pozwala nam mówić o algebrach jako typu τ z pojedynczą funkcją od pewnego bałaganu Either s do pojedynczego τ. Dla monoidów ten bałagan to: Either (τ, τ) (); dla grup (które mają dodatkową operację τ → τ) to: Either (Either (τ, τ) τ) (). To inny typ dla każdej innej struktury. Więc co te wszystkie typy mają ze sobą wspólnego? Najbardziej oczywistą rzeczą jest to, że wszystkie są tylko sumami produktów-algebraicznymi typami danych. Na przykład dla monoidów możemy utworzyć monoid typ argumentu, który działa dla any monoid τ:
data MonoidArgument τ = Mappend τ τ -- here τ τ is the same as (τ, τ)
| Mempty -- here we can just leave the () out
Możemy zrobić to samo dla grup, pierścieni, krat i wszystkich innych możliwych struktur.
Co jeszcze jest specjalnego w tych wszystkich typach? Cóż, wszystkie są Functors! Np.:
instance Functor MonoidArgument where
fmap f (Mappend τ τ) = Mappend (f τ) (f τ)
fmap f Mempty = Mempty
τ z funkcją f τ → τ dla jakiegoś functora f. W rzeczywistości możemy to zapisać jako typeklasa:
class Functor f ⇒ Algebra f τ where
op ∷ f τ → τ
To jest często nazywana "f-algebrą", ponieważ jest określona przez funktor F. Gdybyśmy mogli częściowo zastosować typeklasy, moglibyśmy zdefiniować coś w rodzaju class Monoid = Algebra MonoidArgument.
Coalgebras
Teraz, mam nadzieję, że dobrze rozumiesz, czym jest algebra i jak to jest tylko uogólnienie normalnych struktur algebraicznych. Czym jest F-coalgebra? Cóż, co oznacza, że jest to "dualne" algebry-czyli bierzemy algebrę i rzucamy strzałkami. Widzę tylko jedną strzałkę w powyższym definicja, więc po prostu to odwrócę:
class Functor f ⇒ CoAlgebra f τ where
coop ∷ τ → f τ
I to wszystko! Teraz ten wniosek może wydawać się trochę niepoważny (heh). Mówi ci czym jest coalgebra, ale tak naprawdę nie daje żadnego wglądu w to, jak jest przydatna lub dlaczego nam zależy. Jak tylko znajdę lub wymyślę dobry przykład lub dwa :P.
Klasy i Obiekty
Po przeczytaniu trochę, myślę, że mam dobry pomysł, jak używać coalgebras do reprezentowania klas i obiektów. Mamy Typ C, który zawiera wszystkie możliwe stany wewnętrzne obiektów w klasie; klasa sama w sobie jest coalgebrą nad C, która określa metody i właściwości obiektów.
Jak pokazano na przykładzie algebry, jeśli mamy kilka funkcji takich jak a → τ i b → τ dla dowolnych a, b,…, możemy połączyć je wszystkie w jedną funkcję za pomocą Either, typu suma. Podwójnym "pojęciem" byłoby łączenie kilku funkcji typu τ → a, τ → b i tak dalej. Możemy zrób to za pomocą dwójki typu sumy-typu produktu A. Tak więc, biorąc pod uwagę dwie powyższe funkcje (nazwane f i g), możemy utworzyć jedną w ten sposób:
both ∷ τ → (a, b)
both x = (f x, g x)
Typ (a, a) jest funktorem w prosty sposób, więc z pewnością pasuje do naszego pojęcia f-coalgebra. Ta konkretna sztuczka pozwala nam spakować kilka różnych funkcji-lub, dla OOP, metod - w jedną funkcję typu {62]}.
Elementy naszego typu C reprezentują wewnętrzny stan obiektu. Jeśli obiekt ma jakieś czytelne właściwości, muszą one zależeć od stanu. Najbardziej oczywistym sposobem na to jest uczynienie z nich funkcji C. Jeśli więc chcemy mieć właściwość length (np. object.length), Mamy funkcję C → Int.
Chcemy metod, które mogą pobierać argument i modyfikować stan. Aby to zrobić, musimy wziąć wszystkie argumenty i stworzyć nowy C. Wyobraźmy sobie metodę setPosition, która przyjmuje x i y współrzędne: object.setPosition(1, 2). Wyglądałoby to tak: C → ((Int, Int) → C).
Ważnym wzorcem jest to, że "metody" i "właściwości" obiektu przyjmują sam obiekt jako swój pierwszy argument. Jest to tak samo jak parametr self w Pythonie i jak domyślna this w wielu innych językach. Coalgebra zasadniczo zawiera zachowanie biorąc self parametr: to jest to, co pierwszy C w C → F C jest.
position właściwość, a name właściwość i setPosition funkcja:
class C
private
x, y : Int
_name : String
public
name : String
position : (Int, Int)
setPosition : (Int, Int) → C
Potrzebujemy dwóch części do reprezentowania tej klasy. Po pierwsze, musimy reprezentować wewnętrzny stan obiektu; w tym przypadku posiada on tylko dwa Int s I String. (To jest nasz Typ C./ Align = "center" bgcolor = "# e0ffe0 " / cesarz Chin / / align = center /
data C = Obj { x, y ∷ Int
, _name ∷ String }
Mamy dwie właściwości do zapisania. Są dość trywialne:
position ∷ C → (Int, Int)
position self = (x self, y self)
name ∷ C → String
name self = _name self
Teraz musimy być w stanie zaktualizować pozycja:
setPosition ∷ C → (Int, Int) → C
setPosition self (newX, newY) = self { x = newX, y = newY }
To jest jak Klasa Pythona z jej jawnymi zmiennymi self. Teraz, gdy mamy kilka funkcji self →, musimy połączyć je w jedną funkcję dla coalgebry. Możemy to zrobić za pomocą prostej krotki:
coop ∷ C → ((Int, Int), String, (Int, Int) → C)
coop self = (position self, name self, setPosition self)
Typ ((Int, Int), String, (Int, Int) → c)-dla dowolny c-jest funktorem, więc coop ma żądaną formę: Functor f ⇒ C → f C.
Biorąc to pod uwagę, C wraz z coop tworzą coalgebra, która określa klasę, którą podałem powyżej. Zobacz też jak możemy użyć tej samej techniki, aby określić dowolną liczbę metod i właściwości, które mają mieć nasze obiekty.
To pozwala nam używać rozumowania coalgebraic do radzenia sobie z klasami. Na przykład, możemy wprowadzić pojęcie "homomorfizmu f-coalgebra" do reprezentowania przekształceń między klasami. Jest to przerażająco brzmiące określenie, które oznacza po prostu transformację między węglami, która zachowuje strukturę. To znacznie ułatwia myślenie o mapowaniu klas na inne klasy.
W skrócie, F-coalgebra reprezentuje klasę, posiadając kilka właściwości i metod, które zależą od parametru self zawierającego wewnętrzny stan każdego obiektu.
Inne Kategorie
Do tej pory mówiliśmy o algebrach i węglgebrach jako typach Haskella. Algebra jest tylko typem τ z funkcją f τ → τ, a coalgebra jest tylko typem {[14] } z funkcją τ → f τ.
Jednak nic tak naprawdę nie łączy tych pomysłów z Haskellem per se . W rzeczywistości są one zwykle wprowadzane w kategoriach zbiorów i funkcji matematycznych, a nie typów i funkcji Haskella. Rzeczywiście, możemy uogólnić te pojęcia do dowolnych kategorii!
Możemy zdefiniować f-algebrę dla pewnej kategorii C. Po pierwsze, potrzebujemy functor F : C → C-czyli endofunctor . (Wszystkie Haskell FunctorS są w rzeczywistości endofunkcjami z Hask → Hask.) Wtedy algebra jest tylko obiektem A z C Z morfizmem F A → A. A coalgebra jest taka sama, z wyjątkiem A → F A.
Co zyskujemy rozważając inne kategorie? Możemy użyć tych samych pomysłów w różnych kontekstach. Jak monady. W Haskell monada to rodzaj M ∷ ★ → ★ z trzema operacjami:
map ∷ (α → β) → (M α → M β)
return ∷ α → M α
join ∷ M (M α) → M α
Funkcja map jest tylko dowodem na to, że M jest Functor. Można więc powiedzieć, że monada jest tylko funktorem z dwoma operacjami: return i join.
Funktory same tworzą kategorię, z morfizmy między nimi są tzw. "naturalnymi transformacjami". Transformacja naturalna to tylko sposób na przekształcenie jednego funktora w inny przy zachowaniu jego struktury. oto fajny artykuł, który pomoże wyjaśnić ten pomysł. Mówi o concat, czyli po prostu join dla list.
W przypadku funktorów Haskella skład dwóch funktorów jest funktorem samym w sobie. W pseudokodzie możemy napisać:
instance (Functor f, Functor g) ⇒ Functor (f ∘ g) where
fmap fun x = fmap (fmap fun) x
To pomaga nam myśleć o join jako o mapowaniu z f ∘ f → f. Typ join to ∀α. f (f α) → f α. Intuicyjnie możemy zobaczyć, jak funkcję ważną dla wszystkich typów α można traktować jako przekształcenie f.
return jest podobną transformacją. Jego typ to ∀α. α → f α. To wygląda inaczej-pierwszy α nie jest "w" functorze! Na szczęście możemy to naprawić, dodając tam funktor tożsamości: {122]}. Więc return jest transformacją Identity → f.
Teraz możemy myśleć o monadzie jako o algebrze opartej na niektóre funkcje f z operacjami f ∘ f → f i Identity → f. Czy to nie wygląda znajomo? Jest bardzo podobny do monoidu, który był tylko pewnym typem τ z operacjami τ × τ → τ i () → τ.
Więc monada jest jak monoid, tyle że zamiast typu mamy funktor. To ten sam rodzaj algebry, tylko w innej kategorii. (To stąd z tego co wiem pochodzi fraza "monada to tylko monoid w kategorii endofunktorów".)
Teraz mamy te dwa operacje: f ∘ f → f i Identity → f. Aby uzyskać odpowiednią coalgebrę, po prostu odwracamy strzałki. To daje nam dwie nowe operacje: f → f ∘ f i f → Identity. Możemy przekształcić je w typy Haskell dodając zmienne typu jak powyżej, dając nam ∀α. f α → f (f α) i ∀α. f α → α. W związku z tym, że nie jest to możliwe, nie jest to możliwe.]}
class Functor f ⇒ Comonad f where
coreturn ∷ f α → α
cojoin ∷ f α → f (f α)
Więc comonad jest wtedy } coalgebra w kategorii endofunktorów.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2013-05-07 16:26:57
F-algebry i F-coalgebry są strukturami matematycznymi, które odgrywają kluczową rolę w rozumowaniu o typach indukcyjnych (lub typach rekurencyjnych).
F-algebry
Zaczniemy od F-algebr. Postaram się być jak najprostszy.
Domyślam się, że wiesz co to jest typ rekurencyjny. Na przykład jest to typ dla listy liczb całkowitych:
data IntList = Nil | Cons (Int, IntList)
Jest oczywiste, że jest rekurencyjny - w rzeczy samej, jego definicja odnosi się do siebie. Jego definicja składa się z dwóch konstruktorów danych, które mają następujące typy:
Nil :: () -> IntList
Cons :: (Int, IntList) -> IntList
Zauważ, że napisałem Typ Nil jako () -> IntList, a nie po prostu IntList. Są to w rzeczywistości typy równoważne z teoretycznego punktu widzenia, ponieważ Typ () ma tylko jednego mieszkańca.
Jeśli napiszemy podpisy tych funkcji w bardziej teoretyczny sposób, otrzymamy
Nil :: 1 -> IntList
Cons :: Int × IntList -> IntList
Gdzie 1 jest zbiorem jednostkowym (zbiorem z jednym elementem), a A × B operacja jest krzyżykiem iloczyn dwóch zbiorów A i B (czyli zbiór par (a, b) gdzie a przechodzi przez wszystkie elementy A i b przechodzi przez wszystkie elementy B).
Związek dwóch zbiorów A i B jest zbiorem A | B, który jest związkiem zbiorów {(a, 1) : a in A} i {(b, 2) : b in B}. Zasadniczo jest to zbiór wszystkich elementów z A i B, ale z każdym z tych elementów "oznaczonych" jako należące do A lub B, więc gdy wybierzemy dowolny element z A | B, natychmiast wiedzieć, czy ten element pochodzi z A czy z B.
Możemy 'połączyć' Nil i Cons funkcje, więc utworzą one jedną funkcję działającą na zbiorze 1 | (Int × IntList):
Nil|Cons :: 1 | (Int × IntList) -> IntList
Rzeczywiście, jeśli Nil|Cons funkcja jest zastosowana do wartości () (która oczywiście należy do zbioru 1 | (Int × IntList)), to zachowuje się tak, jakby była Nil; jeśli Nil|Cons jest zastosowana do dowolnej wartości typu (Int, IntList) (takie wartości są również w zbiorze 1 | (Int × IntList), zachowuje się ona jak Cons.
Teraz zastanów się nad innym datatype:
data IntTree = Leaf Int | Branch (IntTree, IntTree)
Ma następujące konstruktory:
Leaf :: Int -> IntTree
Branch :: (IntTree, IntTree) -> IntTree
Które można również połączyć w jedną funkcję:
Leaf|Branch :: Int | (IntTree × IntTree) -> IntTree
Widać, że obie te funkcje mają podobny typ: obie wyglądają jak
f :: F T -> T
Gdzie F jest rodzajem transformacji, która przyjmuje nasz typ i daje bardziej złożony typ, który składa się z operacji x i {67]}, zastosowań T i ewentualnie innych typów. Na przykład dla IntList i IntTree F wygląda jak następuje:
F1 T = 1 | (Int × T)
F2 T = Int | (T × T)
Możemy natychmiast zauważyć, że każdy typ algebraiczny może być zapisany w ten sposób. Rzeczywiście, dlatego nazywa się je "algebraicznymi": składają się z szeregu " Sum "(związków) i "produktów" (produktów krzyżowych) innych typów.
Teraz możemy zdefiniować f-algebrę. f-algebra jest tylko parą (T, f), gdzie T jest pewnym typem, a f jest funkcją typu f :: F T -> T. W naszych przykładach f-algebry to (IntList, Nil|Cons) i (IntTree, Leaf|Branch). Należy jednak pamiętać, że pomimo tego typu f funkcja jest taka sama dla każdego F, T i f same mogą być dowolne. Na przykład, (String, g :: 1 | (Int x String) -> String) lub (Double, h :: Int | (Double, Double) -> Double) dla niektórych g i h są również algebrami F dla odpowiadających im F.
Następnie możemy wprowadzić homomorfizmy f-algebry , a następnie początkowe f-algebry , które mają bardzo użyteczne właściwości. W rzeczywistości (IntList, Nil|Cons) jest początkową algebrą F1, a (IntTree, Leaf|Branch) jest początkową algebrą F2. Nie będę przedstawiał dokładnych definicji tych terminów i właściwości, ponieważ są bardziej złożone i abstrakcyjne niż to konieczne.
Niemniej jednak fakt, że powiedzmy, (IntList, Nil|Cons) jest F-algebrą pozwala nam zdefiniować fold funkcję podobną do tego typu. Jak wiesz, fold jest rodzajem operacji, która przekształca jakiś rekurencyjny typ danych w jedną skończoną wartość. Na przykład, możemy złożyć listę liczb całkowitych w jedną wartość, która jest sumą wszystkich elementów na liście:
foldr (+) 0 [1, 2, 3, 4] -> 1 + 2 + 3 + 4 = 10
Możliwe jest uogólnienie takiej operacji na dowolnym rekurencyjnym typie danych.
The poniżej znajduje się podpis foldr funkcji:
foldr :: ((a -> b -> b), b) -> [a] -> b
Zauważ, że użyłem szelek do oddzielenia dwóch pierwszych argumentów od ostatniego. Nie jest to funkcja prawdziwa foldr, ale jest do niej izomorficzna (czyli można łatwo uzyskać jedną od drugiej i odwrotnie). Częściowo zastosowany foldr będzie miał następujący podpis:
foldr ((+), 0) :: [Int] -> Int
Widzimy, że jest to funkcja, która pobiera listę liczb całkowitych i zwraca pojedynczą liczbę całkowitą. Zdefiniujmy taką funkcję w kategoriach naszego IntList Typ.
sumFold :: IntList -> Int
sumFold Nil = 0
sumFold (Cons x xs) = x + sumFold xs
Widzimy, że ta funkcja składa się z dwóch części: pierwsza część definiuje zachowanie tej funkcji na Nil Części IntList, a druga część definiuje zachowanie funkcji na Cons części.
Teraz Załóżmy, że programujemy Nie w Haskell, ale w jakimś języku, który pozwala na użycie typów algebraicznych bezpośrednio w podpisach typów (cóż, technicznie Haskell pozwala na użycie typów algebraicznych za pomocą krotek i {96]} datatype, ale to doprowadzi do niepotrzebnego verbosity). Rozważmy funkcję:
reductor :: () | (Int × Int) -> Int
reductor () = 0
reductor (x, s) = x + s
Widać, że reductor jest funkcją typu F1 Int -> Int, tak jak w definicji f-algebry! W rzeczywistości para (Int, reductor) jest algebrą F1.
Ponieważ IntList jest początkową algebrą F1, dla każdego typu T i dla każdej funkcji r :: F1 T -> T istnieje funkcja, zwana katamorfizmem dla r, która przekształca IntList na T, i taka funkcja jest unikalna. Rzeczywiście, w naszym przykładzie katamorfizm dla reductor to sumFold. Uwaga jak reductor i sumFold są podobne: mają prawie taką samą strukturę! W reductor definicja s użycie parametru (którego typ odpowiada T) odpowiada wykorzystaniu wyniku obliczeń sumFold xs w definicji sumFold.
Aby było to bardziej jasne i pomóc ci zobaczyć wzór, oto kolejny przykład i ponownie zaczynamy od wynikowej funkcji składania. Rozważmy append funkcję, która dodaje swój pierwszy argument do drugiego:
(append [4, 5, 6]) [1, 2, 3] = (foldr (:) [4, 5, 6]) [1, 2, 3] -> [1, 2, 3, 4, 5, 6]
This how wygląda na nasze IntList:
appendFold :: IntList -> IntList -> IntList
appendFold ys () = ys
appendFold ys (Cons x xs) = x : appendFold ys xs
Spróbujmy jeszcze raz napisać reduktor:
appendReductor :: IntList -> () | (Int × IntList) -> IntList
appendReductor ys () = ys
appendReductor ys (x, rs) = x : rs
appendFold jest katamorfizmem dla appendReductor, który przekształca IntList w IntList.
Tak więc, zasadniczo, f-algebry pozwalają nam definiować 'fałdy' na rekurencyjnych strukturach danych, czyli operacje, które redukują nasze struktury do pewnej wartości.
F-coalgebras
F-coalgebry są tak zwanymi "podwójnymi" terminami dla F-algebr. Pozwalają nam zdefiniować unfolds dla rekurencyjnego typy danych, czyli sposób konstruowania rekurencyjnych struktur z pewnej wartości.
Załóżmy, że masz następujący typ:
data IntStream = Cons (Int, IntStream)
Jest to nieskończony strumień liczb całkowitych. Jego jedyny konstruktor ma następujący typ:
Cons :: (Int, IntStream) -> IntStream
Lub w kategoriach zbiorów
Cons :: Int × IntStream -> IntStream
Haskell pozwala dopasować wzorce na konstruktorach danych, dzięki czemu można zdefiniować następujące funkcje działające na IntStream s:
head :: IntStream -> Int
head (Cons (x, xs)) = x
tail :: IntStream -> IntStream
tail (Cons (x, xs)) = xs
Można naturalnie "połączyć" te funkcje w funkcja pojedyncza typu IntStream -> Int × IntStream:
head&tail :: IntStream -> Int × IntStream
head&tail (Cons (x, xs)) = (x, xs)
Zauważ, jak wynik funkcji pokrywa się z algebraiczną reprezentacją naszego typu IntStream. Podobne rzeczy można również zrobić dla innych rekurencyjnych typów danych. Może już zauważyłeś wzór. Mam na myśli rodzinę funkcji typu
g :: T -> F T
Gdzie T jest jakimś typem. Od teraz będziemy definiować
F1 T = Int × T
Teraz, F-coalgebra jest parą (T, g), gdzie T jest typem, a g jest funkcja typu g :: T -> F T. Na przykład, (IntStream, head&tail) jest F1-coalgebra. Ponownie, podobnie jak w algebrach F, g i T mogą być dowolne, na przykład (String, h :: String -> Int x String) jest również koalgebrą F1 dla niektórych h.
Wśród wszystkich F-coalgebras istnieją tak zwane końcowe f-coalgebras, które są podwójne do początkowych f-algebr. Na przykład IntStream jest terminalem F-coalgebra. Oznacza to, że dla każdego typu T i dla każdej funkcji p :: T -> F1 T istnieje funkcja o nazwie anamorfizm , która przekształca T na IntStream, a taka funkcja jest unikalna.
Rozważmy następującą funkcję, która generuje strumień kolejnych liczb całkowitych zaczynających się od podanej:
nats :: Int -> IntStream
nats n = Cons (n, nats (n+1))
Przyjrzyjmy się teraz funkcji natsBuilder :: Int -> F1 Int, czyli, natsBuilder :: Int -> Int × Int:
natsBuilder :: Int -> Int × Int
natsBuilder n = (n, n+1)
Ponownie widzimy pewne podobieństwo między nats i natsBuilder. Jest to bardzo podobne do połączenia, które obserwowaliśmy wcześniej z reduktorami i fałdami. nats jest anamorfizmem dla natsBuilder.
iterate :: (Int -> Int) -> Int -> IntStream
iterate f n = Cons (n, iterate f (f n))
Jego funkcja budownicza jest następująca:
iterateBuilder :: (Int -> Int) -> Int -> Int × Int
iterateBuilder f n = (n, f n)
Wtedy iterate jest anamorfizmem dla iterateBuilder.
Podsumowanie
W skrócie, f-algebry pozwalają definiować fałdy, czyli operacje redukujące strukturę rekurencyjną do jednej wartości, A F-algebry pozwalają na przeciwny: skonstruować [potencjalnie] nieskończoną strukturę z jednej wartości.
W rzeczywistości w algebrach Haskella F I F-coalgebras pokrywają się. Jest to bardzo ładna właściwość, która jest konsekwencją obecności "dolnej" wartości w każdym typie. Tak więc w Haskell zarówno fałdy i rozkłada mogą być tworzone dla każdego typu rekurencyjnego. Jednak teoretyczny model stojący za tym jest bardziej złożony niż ten, który przedstawiłem powyżej, więc celowo go unikałem.
Mam nadzieję, że to pomoże.Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-10-03 05:00:43
Przechodzenie przez samouczek samouczek o algebrach (co) i indukcji (co) powinien dać ci trochę wglądu w co-algebrę w informatyce.
Poniżej cytat z tego, aby cię przekonać,
Ogólnie rzecz biorąc, program w niektórych językach programowania manipuluje danymi. Podczas rozwoju informatyki w ciągu ostatnich kilkudziesięciu lat stało się jasne, że streszczenie opis tych danych jest pożądany, na przykład w celu zapewnienia, że czyjeś program nie zależy od konkretnej reprezentacji danych, na których działa. Ponadto taka abstrakcyjność ułatwia dowody poprawności.
Pragnienie to doprowadziło do wykorzystania metod algebraicznych w informatyce, w gałęzi zwanej specyfikacją algebraiczną lub abstrakcyjną teorią typów danych. Przedmiotem badań są same w sobie typy danych, wykorzystujące pojęcia technik znanych z algebry. Typy danych wykorzystywane przez informatyków są często generowane z danego zbioru (konstruktor) operacji i to właśnie z tego powodu "inicjalność" algebr odgrywa tak ważną rolę.
Standardowe techniki algebraiczne okazały się przydatne w przechwytywaniu różnych istotnych aspektów struktur danych stosowanych w informatyce. Okazało się jednak, że trudno algebraicznie opisać niektóre z naturalnie dynamicznych struktur występujących w informatyce. Takie struktury zwykle wiążą się z pojęciem państwa, które można przekształcić na różne sposoby. Formalne podejście do takich systemy dynamiczne oparte na stanie zazwyczaj wykorzystują automaty lub systemy przejściowe, jako klasyczne wczesne odniesienia.
W ciągu ostatniej dekady stopniowo rosło przekonanie, że takie systemy oparte na stanie nie powinny być opisywane jako algebry, ale jako tak zwane co-algebry. Są to formalne dwójki algebr, w sposób, który zostanie precyzyjny w tym tutorialu. Dualna własność "inicjalności" dla algebr, a mianowicie skończoności okazała się kluczowa dla takich co-algebr. I logiczne zasada rozumowania, która jest potrzebna dla takich końcowych co-algebr, nie jest indukcją, ale co-indukcją.
Preludium, o teorii kategorii. Teoria kategorii powinna być przemianowana na teorię funktorów. Ponieważ kategorie są tym, co należy zdefiniować, aby zdefiniować funktory. (Co więcej, funktory są tym, co trzeba zdefiniować, aby zdefiniować przekształcenia naturalne.)
Co to jest funkcjonariusz? Jest transformacją z jednego zestawu do drugiego, która zachowuje ich struktura. (Po więcej szczegółów jest dużo dobrego opisu w sieci).
Co to jest F-algebra? To algebra funktora. To tylko badanie uniwersalnej poprawności funkcjonariusza.
Jak to może być link do informatyki ? Program może być wyświetlany jako uporządkowany zestaw informacji. Wykonanie programu odpowiada modyfikacji tego uporządkowanego zbioru informacji. Dobrze, że wykonanie powinno zachować strukturę programu. Wtedy wykonanie może być postrzegane jako zastosowanie functora nad tym zbiorem informacji. (Ten definiujący program).
Dlaczego F-co-algebra ? Programy są dualistyczne z istoty, ponieważ są one opisywane przez informacje i działają na nim. Wtedy głównie informacje, które tworzą program i sprawiają, że są zmieniane, mogą być wyświetlane w dwojaki sposób.
- dane, które można zdefiniować jako informacje przetwarzane przez program.
- Stan, który można zdefiniować jako informację będącą udostępniony przez program.
Wtedy na tym etapie, chciałbym powiedzieć, że,
- F-algebra jest badaniem transformacji funkcjonalnej działającej nad wszechświatem danych(jak tu zdefiniowano).
- F-co-algebry to badanie transformacji funkcjonalnej działającej na wszechświat Państwa(jak tu zdefiniowano).
Podczas życia programu Dane i państwa współistnieją i uzupełniają się nawzajem. Są podwójne.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2013-04-21 20:12:07
Zacznę od rzeczy, które są oczywiście związane z programowaniem, a następnie dodam trochę matematyki, aby utrzymać to tak konkretne i przyziemne, jak tylko mogę.
Zacytujmy kilku informatyków na temat coindukcji...]}
Http://www.cs.umd.edu/~micinski/posts/2012-09-04-on-understanding-coinduction.html
Indukcja jest o skończonych danych, co-indukcja jest o nieskończonych danych.
Typowym przykładem nieskończonych danych jest typ z leniwej listy (a stream). Przykładowo, powiedzmy, że mamy następujący obiekt w pamięć:
let (pi : int list) = (* some function which computes the digits of
π. *)
Komputer nie może pomieścić wszystkich π, ponieważ ma tylko skończoną ilość pamięci! Ale to, co może zrobić, to posiadać skończony program, który będzie twórz dowolnie długie rozszerzenie π, które pragniesz. As long ponieważ używasz tylko skończonych fragmentów listy, możesz obliczyć z tego nieskończona lista tyle, ile potrzebujesz.
Jednak należy wziąć pod uwagę następujący program:
let print_third_element (k : int list) = match k with
| _ :: _ :: thd :: tl -> print thd
print_third_element pi
Ten program powinien wydrukować trzecia cyfra pi. Ale w niektórych językach każdy argument do funkcji jest oceniany przed przekazaniem w funkcję (ścisłą, nie leniwą, ewaluacyjną). Jeśli użyjemy tego zamówienie redukcji, wtedy nasz powyższy program będzie działał na zawsze cyfr pi przed przekazaniem go do naszej funkcji drukarki (która nigdy się nie zdarza). Ponieważ maszyna nie ma nieskończonej pamięci, program w końcu uruchomi się z pamięci i krachu. To może nie być najlepsza kolejność oceny.
Http://adam.chlipala.net/cpdt/html/Coinductive.html
W leniwych funkcyjnych językach programowania, takich jak Haskell, nieskończone struktury danych są wszędzie. Nieskończone listy i bardziej egzotyczne typy danych zapewniają wygodne abstrakcje do komunikacji między częściami programu. Osiąganie podobnych wygoda bez nieskończonych leniwych struktur wymagałaby w wielu przypadkach akrobatyczne inwersje przepływu sterowania.
Http://www.alexandrasilva.org/#/talks.html
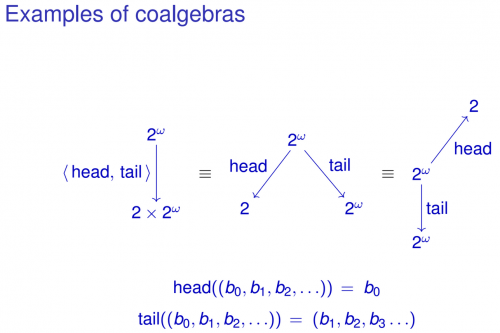
Powiązanie kontekstu matematycznego otoczenia ze zwykłymi zadaniami programistycznymi
Co to jest "algebra"?
Struktury algebraiczne na ogół wyglądają następująco:
- rzeczy
- What the stuff can do
To powinno brzmieć jak obiekty z 1. właściwości i 2. metody. A nawet lepiej, powinien brzmieć jak typ podpisy.
Standardowe przykłady matematyczne obejmują monoid ⊃ Grupa ⊃ wektor-przestrzeń ⊃ "algebra". Monoidy są jak automaty: sekwencje czasowników (np. f.g.h.h.nothing.f.g.f). git log, który zawsze dodaje historię i nigdy nie usuwa, byłby monoidem, ale nie grupą. Jeśli dodasz odwrotności (np. liczby ujemne, ułamki, korzenie, usuwanie nagromadzonej historii, rozbijanie zepsutego lustra), otrzymasz grupę.
Grupy zawierają rzeczy, które można dodawać lub odejmować razem. Na przykład Durations można dodawać razem. (Ale Date s nie może.) Czasowniki żyją w przestrzeni wektorowej (nie tylko w grupie), ponieważ mogą być skalowane również przez liczby zewnętrzne. (Podpis typu scaling :: (Number,Duration) → Duration.)
Algebry ⊂ przestrzenie wektorowe mogą zrobić jeszcze jedną rzecz: jest kilka m :: (T,T) → T. Nazywaj to "mnożeniem" lub nie, ponieważ gdy już opuścisz Integers, mniej oczywiste jest, czym powinno być "mnożenie" (lub "wykładnictwo").
(dlatego ludzie patrzą na (kategoria-teoretyczne) uniwersalne właściwości: aby powiedz im, co mnożenie powinno robić lub być jak :
 )
)
Algebry → Coalgebras
Komultiplikacja jest łatwiejsza do zdefiniowania w sposób, który wydaje się nie arbitralny, niż mnożenie, ponieważ aby przejść od T → (T,T) można po prostu powtórzyć ten sam element. ("diagonal map – - podobne macierze/operatory diagonalne w teorii spektralnej)
Counit jest zwykle śladem (sumą przekątnych wpisów) , chociaż znowu ważne jest to, co twoje counit robi; trace to po prostu dobra odpowiedź dla matryc.
Powodem, aby spojrzeć na przestrzeń podwójną , w ogóle, jest to, że łatwiej jest myśleć w tej przestrzeni. Na przykład czasami łatwiej jest myśleć o wektorze normalnym niż o płaszczyźnie, do której jest to normalne, ale można kontrolować płaszczyzny (w tym hiperplanes) za pomocą wektorów(a teraz mówię o znanym wektorze geometrycznym, jak w ray-tracer).
Oswajanie (nie)ustrukturyzowane dane
Matematycy mogą modelować coś fajnego jak TQFT ' s, podczas gdy programiści muszą zmagać się z
- daty/godziny (
+ :: (Date,Duration) → Date), - miejsca (
Paris≠(+48.8567,+2.3508)! To kształt, nie Punkt.), - niestrukturalny JSON, który ma być w pewnym sensie spójny,
- wrong-but-close XML,
- niezwykle złożone dane GIS, które powinny zaspokoić masę sensownych relacji,
- wyrażenia regularne, które oznaczało coś dla ciebie, ale znaczyło znacznie mniej dla Perla. CRM, który powinien zawierać wszystkie numery telefonów i lokalizacje willi dyrektora, imiona jego (teraz byłej) żony i dzieci, urodziny i wszystkie poprzednie prezenty, z których każdy powinien zaspokoić "oczywiste" relacje (oczywiste dla klienta), które są niezwykle trudne do zakodowania,]}
- .....
Informatycy, mówiąc o węglu, zwykle mają na myśli operacje, jak Kartezjusz produkt. Wierzę, że to właśnie ludzie mają na myśli, gdy mówią: "algebry to coalgebry w Haskell". Ale do tego stopnia, że programiści muszą modelować złożone typy danych, takie jakPlace, Date/Time, i Customer-i sprawić, by te modele wyglądały jak najbardziej jak świat rzeczywisty (a przynajmniej pogląd użytkownika końcowego na świat rzeczywisty)-wierzę, że Duale mogą być przydatne poza tylko set-world.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-10-03 00:45:07