Najszybsza implementacja sinusa, cosinusa i pierwiastka kwadratowego w C++ (nie musi być zbyt dokładna)
Googluję pytanie za ostatnią godzinę, ale są tylko punkty do serii Taylora lub jakiegoś przykładowego kodu, który albo jest zbyt wolny, albo w ogóle się nie kompiluje. Cóż, większość odpowiedzi, które znalazłem w Google to "Google to, to już zapytał", ale niestety to nie ...
Profiluję swoją grę na low-Endzie Pentium 4 i dowiedziałem się, że ~85% czasu wykonania marnuje się na obliczanie sinusa, cosinusa i pierwiastka kwadratowego (ze standardowej biblioteki C++ w Visual Studio), a to wydaje się być mocno zależny od procesora (na moim I7 te same funkcje dostały tylko 5% czasu wykonania, a gra jest waaaaaaaaay szybsza). Nie mogę zoptymalizować tych trzech funkcji, ani obliczyć sinusa i cosinusa w jednym przejściu (nie ma zależności), ale nie potrzebuję zbyt dokładnych wyników do mojej symulacji, więc mogę żyć z szybszym przybliżeniem.
Zatem pytanie: jaki jest najszybszy sposób na obliczenie sinusa, cosinusa i pierwiastka kwadratowego dla float in C++?
EDIT Tabele wyszukiwania są bardziej bolesne, ponieważ wynikający z tego Brak pamięci podręcznej jest o wiele bardziej kosztowny na nowoczesnym procesorze niż seria Taylor. Procesory są teraz tak szybkie, a pamięć podręczna nie.
Popełniłem błąd, pomyślałem, że muszę obliczyć kilka współczynników dla szeregów Taylora i widzę, że teraz Można je zaimplementować jako stałe.
Więc zaktualizowane pytanie: czy jest jakaś szybka Optymalizacja dla pierwiastka kwadratowego, jak również?
EDIT2
Używam pierwiastek kwadratowy do obliczenia odległości, a nie normalizacji - nie można użyć szybkiego algorytmu odwrotnego pierwiastka kwadratowego (jak wskazano w komentarzu: http://en.wikipedia.org/wiki/Fast_inverse_square_root
EDIT3
Nie mogę również operować na odległościach do kwadratu, potrzebuję dokładnej odległości do obliczeń
16 answers
Najszybszym sposobem jest wstępne obliczenie wartości za pomocą tabeli, jak w tym przykładzie:
Tworzenie tabeli Sine lookup w C++
Ale jeśli nalegasz na obliczanie w czasie wykonywania, możesz użyć rozszerzenia szeregów Taylora sinusa lub cosinusa...
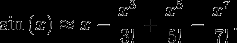
Więcej o serii Taylor... http://en.wikipedia.org/wiki/Taylor_series
Jednym z kluczy do tego, aby to dobrze działało, jest wstępne obliczenie faktorii i obcięcie w rozsądnej liczbie warunki. Faktorie rosną w mianowniku bardzo szybko, więc nie trzeba nosić więcej niż kilka terminów.
Również...Nie mnożyć x^n Od początku za każdym razem...np. pomnóż x^3 przez X kolejne dwa razy, a następnie to przez kolejne dwa, aby obliczyć wykładniki.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-05-23 12:34:38
Oto gwarantowana najszybsza możliwa funkcja sinusoidalna w C++:
double FastSin(double x)
{
return 0;
}
double FastSin(double x)
{
return x;
}
Ta ODPOWIEDŹ w rzeczywistości nie jest do bani , Gdy X jest bliskie zeru. dla małego x, sin(x) jest w przybliżeniu równy x, ponieważ x jest pierwszym terminem Taylora ekspansji sin (x).
Wciąż nie jesteś wystarczająco dokładny? Czytaj dalej. Inżynierowie w latach 70. niektóre fantastyczne odkrycia w tej dziedzinie, ale nowi programiści są po prostu nieświadomi, że te metody istnieją, ponieważ nie są one nauczane w ramach standardowych programów nauczania informatyki.Musisz zacząć od zrozumienia, że nie ma "doskonałej" implementacji tych funkcji dla wszystkich aplikacji. Dlatego powierzchowne odpowiedzi na pytania takie jak "który jest najszybszy" są gwarantowane, że będą błędne.
Większość ludzi, którzy zadają to pytanie, nie rozumie znaczenia z [[17]}kompromisów między wydajnością a dokładnością. W szczególności, będziesz musiał dokonać pewnych wyborów dotyczących dokładności obliczeń, zanim zrobisz cokolwiek innego. Ile błędów można tolerować w wyniku? 10^-4? 10^-16?Jeśli nie możesz oszacować błędu w dowolnej metodzie, nie używaj go. Zobacz wszystkie te losowe Odpowiedzi poniżej moich, które zamieszczają kilka losowych, nieakcentowanych kodów źródłowych, bez wyraźnego udokumentowania zastosowanego algorytmu i jego dokładny maksymalny błąd w zakresie wejściowym? "Błąd jest w przybliżeniu rodzajem Mambo Mambo, zgaduję."To ściśle Liga Busha. jeśli nie wiesz, jak obliczyć dokładny maksymalny błąd, do pełnej precyzji, w funkcji aproksymacji, w całym przedziale wejść... wtedy nie wiesz jak napisać funkcję przybliżenia!
Nikt nie używa samej serii Taylora do przybliżania transcendentalnych w oprogramowanie. Z wyjątkiem pewnych bardzo specyficznych przypadków , szereg Taylora na ogół powoli zbliża się do celu W wspólnych zakresach wejściowych.
Algorytmy, których twoi dziadkowie używali do efektywnego obliczania transcendentalnych, są zbiorczo określane jako CORDIC i były wystarczająco proste, aby można je było zaimplementować w sprzęcie. Oto dobrze udokumentowana implementacja Kordyliery w C . Implementacje CORDIC zazwyczaj wymagają bardzo małej tabeli wyszukiwania, ale większość implementacje nie wymagają nawet, aby dostępny był mnożnik sprzętowy. Większość implementacji CORDIC pozwala na wymianę wydajności na dokładność, w tym Tę, którą połączyłem.
Na przestrzeni lat wprowadzono wiele stopniowych ulepszeń do oryginalnych algorytmów CORDIC. Na przykład w zeszłym roku niektórzy naukowcy z Japonii opublikowali artykuł na temat ulepszonego Kordyliery o lepszych kątach obrotu, co zmniejsza wymagane operacje.
Jeśli masz mnożniki sprzętowe siedząc (i prawie na pewno), lub jeśli nie stać Cię na tabelę wyszukiwania, jakiej wymaga CORDIC, zawsze możesz użyć Chebyshev wielomian , aby zrobić to samo. Wielomiany Czebyszewa wymagają mnożenia, ale rzadko jest to problem na nowoczesnym sprzęcie. Lubimy Wielomiany Czebyszewa, ponieważ mają wysoce przewidywalne maksymalne błędy dla danego przybliżenia . Maksimum ostatniego terminu w Wielomianie Czebyszewa, w całym zakresie wejściowym, ogranicza błąd w wynik. I ten błąd staje się mniejszy, gdy Liczba terminów staje się większa. oto jeden przykład wielomianu Czebyszewa dającego przybliżenie sinusoidalne w ogromnym zakresie, ignorując naturalną symetrię funkcji sinusoidalnej i po prostu rozwiązując problem przybliżenia, rzucając na niego więcej współczynników. A oto przykład oszacowania funkcji sinusoidalnej do 5 ULPs. Nie wiesz co to jest ULP? Powinieneś.
Lubimy też Wielomiany Czebyszewa ponieważ błąd w przybliżeniu jest równomiernie rozłożony w zakresie wyjść. Jeśli piszesz wtyczki audio lub robisz cyfrowe przetwarzanie sygnału, Wielomiany Czebyszewa dają tani i przewidywalny efekt ditheringu " za darmo."
Jeśli chcesz znaleźć własne współczynniki wielomianu Czebyszewa w określonym przedziale, wiele bibliotek matematycznych nazywa proces znajdowania tych współczynników " czebyszew pasuje " lub coś w tym stylu.
Pierwiastki kwadratowe, wtedy jak teraz, algorytm Newtona-Raphsona jest zwykle obliczany przy użyciu pewnego wariantu algorytmu Newtona-Raphsona, Zwykle z ustaloną liczbą iteracji. Zwykle, gdy ktoś wykręca "niesamowity nowy" algorytm rootingu kwadratowego, to tylko Newton-Raphson w przebraniu.
Wielomiany Newtona-Raphsona, KORDYKA i Czebyszewa pozwalają zamienić szybkość na dokładność, więc odpowiedź może być tak nieprecyzyjna, jak chcesz.
Wreszcie, kiedy skończysz wszystkie swoje fantazyjne benchmarking i mikro-optymalizacja, upewnij się, że Twoja "szybka" wersja jest rzeczywiście szybsza niż wersja biblioteki. oto typowa implementacja biblioteki fsin () ograniczona domeną od -pi / 4 do pi / 4. I to nie jest tak cholernie powolne.
Ostatnia uwaga dla ciebie: prawie na pewno używasz matematyki IEEE-754 do wykonywania estymacji, a za każdym razem, gdy wykonujesz matematykę IEEE-754 z mnóstwem mnożenia, niektóre niejasne decyzje inżynierskie podjęte dekady temu powrócą do / align = "center" bgcolor = "# e0ffe0 " / cesarz Chin / / align = center / I te błędy zaczynają się małe, ale stają się większe, i większe, i większe! W pewnym momencie swojego życia przeczytaj "co każdy informatyk powinien wiedzieć o liczbach zmiennoprzecinkowych" i miej odpowiednią dawkę strachu. Pamiętaj, że jeśli zaczniesz pisać własne funkcje transcendentalne, będziesz musiał porównać i zmierzyć rzeczywisty błąd wynikający z zaokrąglenia zmiennoprzecinkowego, a nie tylko maksymalny błąd teoretyczny. To nie jest teoretyczny problem; ustawienia kompilacji "fast math" ugryzły mnie w tyłek, na więcej niż jednym projekcie.
Tl:DR; idź do google "przybliżenie sinusoidalne" lub "przybliżenie cosinusa" lub "przybliżenie pierwiastka kwadratowego" lub " teoria przybliżenia ."
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-08-10 02:19:41
Po pierwsze, Seria Taylora nie jest najlepszym / najszybszym sposobem wdrożenia sinus / cos. Nie jest to również sposób, w jaki profesjonalne biblioteki implementują te funkcje trygonometryczne, a znając najlepszą implementację numeryczną, można dostosować dokładność, aby uzyskać bardziej efektywną prędkość. Ponadto problem ten został już szeroko omówiony w StackOverflow. Oto tylko jeden przykład .
Po drugie, duża różnica między starymi / nowymi komputerami wynika z faktu, że nowoczesne Architektura Intela ma jawny kod asemblacji do obliczania elementarnych funkcji trygonometrycznych. Jest to dość trudne do pokonania ich na szybkość wykonania.
Na koniec porozmawiajmy o kodzie na Twoim starym komputerze. Sprawdź implementację GSL GNU scientific library (lub receptur numerycznych), a zobaczysz, że w zasadzie używają one Formuły przybliżenia Czebyszewa.
Przybliżenie Czebyszewa zbiega się szybciej, więc trzeba ocenić mniej terminów. Nie będę tu pisał szczegółów implementacji bo na StackOverflow są już bardzo ładne odpowiedzi. sprawdź ten na przykład . Wystarczy dostosować liczbę terminów w tej serii, aby zmienić równowagę między dokładnością/prędkością.
W przypadku tego typu problemów, jeśli chcesz poznać szczegóły implementacji jakiejś specjalnej funkcji lub metody numerycznej, powinieneś przyjrzeć się kodowi GSL przed dalszą akcją - GSL jest standardową biblioteką numeryczną.
EDIT: możesz poprawić czas wykonania, włączając agresywne flagi optymalizacji zmiennoprzecinkowej w gcc / icc. Zmniejszy to precyzję, ale wydaje się, że jest to dokładnie to, czego chcesz.
EDIT2: możesz spróbować zrobić grubą siatkę sin i użyć procedury gsl (gsl_interp_cspline_periodic dla splajnu z okresowymi warunkami), aby splajnować tę tabelę (splajn zmniejszy błędy w porównaniu do interpolacji liniowej => potrzebujesz mniej punktów na tabeli => mniej miss pamięci podręcznej)!
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-09-08 07:17:29
Dla pierwiastka kwadratowego istnieje podejście zwane przesunięciem bitowym.
Liczba zmiennoprzecinkowa zdefiniowana przez IEEE-754 używa pewnych bitów reprezentujących czasy wielokrotności 2. Niektóre bity są dla reprezentują wartość bazową.
float squareRoot(float x)
{
unsigned int i = *(unsigned int*) &x;
// adjust bias
i += 127 << 23;
// approximation of square root
i >>= 1;
return *(float*) &i;
}
To stały czas obliczający pierwiastek kwadratowy
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2013-09-06 16:46:13
W oparciu o ideę http://forum.devmaster.net/t/fast-and-accurate-sine-cosine/9648 i pewne ręczne przepisywanie w celu poprawy wydajności w mikro benchmarku i skończyło się na następującej implementacji cosine, która jest używana w symulacji fizyki HPC, która jest wąska przez powtarzające się wywołania cos na dużej przestrzeni liczbowej. Jest wystarczająco dokładny i znacznie szybszy niż tabela wyszukiwania, przede wszystkim nie jest wymagany podział.
template<typename T>
inline T cos(T x) noexcept
{
constexpr T tp = 1./(2.*M_PI);
x *= tp;
x -= T(.25) + std::floor(x + T(.25));
x *= T(16.) * (std::abs(x) - T(.5));
#if EXTRA_PRECISION
x += T(.225) * x * (std::abs(x) - T(1.));
#endif
return x;
}
Kompilator Intela jest przynajmniej inteligentny wystarczy wektoryzować tę funkcję, gdy jest używana w pętli.
Jeśli zdefiniowano EXTRA_PRECISION, maksymalny błąd wynosi około 0,00109 dla zakresu-π do π, zakładając, że T jest double, Jak to zwykle jest zdefiniowane w większości implementacji C++. W przeciwnym razie maksymalny błąd wynosi około 0,056 dla tego samego zakresu.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2016-11-20 19:29:02
Dla x86, hardware FP square root instructions są szybkie (sqrtss to sqrt Skalar Single-precision). Pojedyncza precyzja jest szybsza niż Podwójna precyzja, więc zdecydowanie użyj float zamiast double dla kodu, w którym możesz sobie pozwolić na użycie mniejszej precyzji.
Dla 32-bitowego kodu, zwykle potrzebujesz opcji kompilatora, aby wykonać matematykę FP z instrukcjami SSE, a nie x87. (np. -mfpmath=sse)
Aby uzyskać funkcje C sqrt() lub sqrtf() do inline jako tylko sqrtsd lub sqrtss, musisz Kompiluj z -fno-math-errno. Ustawienie funkcji matematycznych errno na NaN jest ogólnie uważane za błąd projektowy, ale Standard tego wymaga. Bez tej opcji, gcc wprowadza ją, ale następnie wykonuje gałąź compare+, aby sprawdzić, czy wynikiem było NaN, a jeśli tak, wywołuje funkcję biblioteki, dzięki czemu może ustawić errno. Jeśli twój program nie sprawdza errno po funkcjach matematycznych, nie ma niebezpieczeństwa użycia -fno-math-errno.
Nie potrzebujesz żadnej z "niebezpiecznych" części -ffast-math, aby uzyskać sqrt i kilka innych funkcji, aby inline lepiej lub w ogóle, ale -ffast-math może zrobić dużą różnicę (np. pozwolić kompilatorowi na auto-wektoryzację w przypadkach, gdy zmienia to wynik, ponieważ matematyka FP nie jest asocjacyjna.
Np. z kompilacją gcc6.3float foo(float a){ return sqrtf(a); }
foo: # with -O3 -fno-math-errno.
sqrtss xmm0, xmm0
ret
foo: # with just -O3
pxor xmm2, xmm2 # clang just checks for NaN, instead of comparing against zero.
sqrtss xmm1, xmm0
ucomiss xmm2, xmm0
ja .L8 # take the slow path if 0.0 > a
movaps xmm0, xmm1
ret
.L8: # errno-setting path
sub rsp, 24
movss DWORD PTR [rsp+12], xmm1 # store the sqrtss result because the x86-64 SysV ABI has no call-preserved xmm regs.
call sqrtf # call sqrtf just to set errno
movss xmm1, DWORD PTR [rsp+12]
add rsp, 24
movaps xmm0, xmm1 # extra mov because gcc reloaded into the wrong register.
ret
Kod Gcc dla sprawy NaN wydaje się zbyt skomplikowany; nie używa nawet zwracanej wartości sqrtf! W każdym razie, to jest rodzaj bałaganu, który można dostać bez -fno-math-errno, dla każdego sqrtf() call site w Twoim program. W większości jest to po prostu nadęty kod i żaden z .L8 bloku nigdy nie uruchomi się przy użyciu sqrt o numerze > = 0.0, ale jest jeszcze kilka dodatkowych instrukcji w szybkiej ścieżce.
Jeśli wiesz, że twoje wejście do sqrt jest niezerowe, możesz użyć szybkiej, ale bardzo przybliżonej instrukcji sqrt, rsqrtps (lub rsqrtss dla wersji skalarnej). Jeden iteracja Newtona-Raphsona zapewnia niemal taką samą precyzję jak sprzęt Instrukcja single-precision sqrt, ale nie do końca.
sqrt(x) = x * 1/sqrt(x), dla x!=0, więc można obliczyć sqrt z rsqrt i mnożenie. Oba są szybkie, nawet na P4 (Czy to było nadal aktualne w 2013)?
Na P4, Może warto użyć rsqrt + iteracja Newtona do zastąpienia pojedynczego sqrt, nawet jeśli nie trzeba niczego przez nią dzielić.
Zobacz także odpowiedź, którą napisałem niedawno o obsłudze zer przy obliczaniu sqrt(x) jako x*rsqrt(x), z Newtonem Iteracja. Włączyłem trochę dyskusji o błędzie zaokrąglania, jeśli chcesz przekonwertować wartość FP na liczbę całkowitą, i linki do innych istotnych pytań.
P4:
-
sqrtss: 23C latency, not pipelined -
sqrtsd: 38C latency, not pipelined -
fsqrt(x87): opóźnienie 43c, nie pipelinowane rsqrtss/mulss: opóźnienie 4c + 6C. Prawdopodobnie jedna na przepustowość 3c, ponieważ najwyraźniej nie potrzebują tej samej jednostki wykonawczej (mmx vs. fp).-
Wersje spakowane SIMD są nieco wolniejsze
Skylake:
-
sqrtss/sqrtps: 12C latency, jeden na przepustowość 3c -
sqrtsd/sqrtpd: 15-16C latency, jeden na przepustowość 4-6C - 14-21cc latency, jeden na przepustowość 4-7c
-
rsqrtss/mulss: opóźnienie 4c + 4C. Jedna na 1C przepustowość. - wersje wektorowe SIMD 128B mają tę samą prędkość. Wersje wektorowe 256b mają nieco większe opóźnienie, prawie połowa przepustowości. Wersja
rsqrtssma pełną wydajność dla wektorów 256b.
Z iteracją Newtona, wersja rsqrt nie jest dużo, jeśli w ogóle jest szybsza.
Numery z eksperymentalnych testów Agnera Foga . Zobacz jego Przewodniki mikroarchitektury, aby zrozumieć, co sprawia, że kod działa szybko lub wolno. Zobacz także linki na x86 tag wiki.
IDK jak najlepiej obliczyć sin / cos. Czytałem, że sprzęt fsin / fcos (i tylko nieznacznie wolniejszy fsincos, który robi oba naraz) nie są najszybszą drogą, ale IDK co jest.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-07-03 11:28:54
QT ma szybkie implementacje sinus (qFastSin) i cosinus (qFastCos), które używają tabeli look up z interpolacją. Używam go w moim kodzie i są szybsze niż std: sin / cos i wystarczająco precyzyjne do tego, czego potrzebuję:
Https://code.woboq.org/qt5/qtbase/src/corelib/kernel/qmath.h.html#_Z8qFastSind
#define QT_SINE_TABLE_SIZE 256
inline qreal qFastSin(qreal x)
{
int si = int(x * (0.5 * QT_SINE_TABLE_SIZE / M_PI)); // Would be more accurate with qRound, but slower.
qreal d = x - si * (2.0 * M_PI / QT_SINE_TABLE_SIZE);
int ci = si + QT_SINE_TABLE_SIZE / 4;
si &= QT_SINE_TABLE_SIZE - 1;
ci &= QT_SINE_TABLE_SIZE - 1;
return qt_sine_table[si] + (qt_sine_table[ci] - 0.5 * qt_sine_table[si] * d) * d;
}
inline qreal qFastCos(qreal x)
{
int ci = int(x * (0.5 * QT_SINE_TABLE_SIZE / M_PI)); // Would be more accurate with qRound, but slower.
qreal d = x - ci * (2.0 * M_PI / QT_SINE_TABLE_SIZE);
int si = ci + QT_SINE_TABLE_SIZE / 4;
si &= QT_SINE_TABLE_SIZE - 1;
ci &= QT_SINE_TABLE_SIZE - 1;
return qt_sine_table[si] - (qt_sine_table[ci] + 0.5 * qt_sine_table[si] * d) * d;
}
LUT i licencja można znaleźć tutaj: https://code.woboq.org/qt5/qtbase/src/corelib/kernel/qmath.cpp.html#qt_sine_table
Te pary funkcji weź radian. LUT obejmuje cały zakres wejściowy 2π. Funkcja interpoluje między wartościami za pomocą różnicy d, używając cosinusa (z podobną interpolacją za pomocą sinusa) jako pochodnej.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-10-29 14:37:38
Dzieląc mój kod, jest to wielomian Szóstego stopnia, nic specjalnego, ale przestawiony, aby uniknąć pows. NA Core i7 jest to 2,3 razy wolniejsze niż standardowa implementacja, choć trochę szybsze dla [0..2 * pi] zakres. Dla starego procesora może to być alternatywa dla standardowego sin / cos.
/*
On [-1000..+1000] range with 0.001 step average error is: +/- 0.000011, max error: +/- 0.000060
On [-100..+100] range with 0.001 step average error is: +/- 0.000009, max error: +/- 0.000034
On [-10..+10] range with 0.001 step average error is: +/- 0.000009, max error: +/- 0.000030
Error distribution ensures there's no discontinuity.
*/
const double PI = 3.141592653589793;
const double HALF_PI = 1.570796326794897;
const double DOUBLE_PI = 6.283185307179586;
const double SIN_CURVE_A = 0.0415896;
const double SIN_CURVE_B = 0.00129810625032;
double cos1(double x) {
if (x < 0) {
int q = -x / DOUBLE_PI;
q += 1;
double y = q * DOUBLE_PI;
x = -(x - y);
}
if (x >= DOUBLE_PI) {
int q = x / DOUBLE_PI;
double y = q * DOUBLE_PI;
x = x - y;
}
int s = 1;
if (x >= PI) {
s = -1;
x -= PI;
}
if (x > HALF_PI) {
x = PI - x;
s = -s;
}
double z = x * x;
double r = z * (z * (SIN_CURVE_A - SIN_CURVE_B * z) - 0.5) + 1.0;
if (r > 1.0) r = r - 2.0;
if (s > 0) return r;
else return -r;
}
double sin1(double x) {
return cos1(x - HALF_PI);
}
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-04-08 16:38:00
Używam poniższego kodu CORDIC do obliczania funkcji trygonometrycznych z poczwórną precyzją. Stała N określa liczbę bitów wymaganej precyzji(np. N = 26 da dokładność pojedynczej precyzji). W zależności od wymaganej dokładności wstępnie obliczona pamięć masowa może być niewielka i zmieści się w pamięci podręcznej. Wymaga tylko operacji dodawania i mnożenia, a także jest bardzo łatwy do wektoryzowania.
Algorytm wstępnie oblicza wartości sin i cos dla 0,5^i, i=1,..., N. Następnie możemy połączyć te wstępnie obliczone wartości, aby obliczyć Sin i cos dla dowolnego kąta do rozdzielczości 0.5^N
template <class QuadReal_t>
QuadReal_t sin(const QuadReal_t a){
const int N=128;
static std::vector<QuadReal_t> theta;
static std::vector<QuadReal_t> sinval;
static std::vector<QuadReal_t> cosval;
if(theta.size()==0){
#pragma omp critical (QUAD_SIN)
if(theta.size()==0){
theta.resize(N);
sinval.resize(N);
cosval.resize(N);
QuadReal_t t=1.0;
for(int i=0;i<N;i++){
theta[i]=t;
t=t*0.5;
}
sinval[N-1]=theta[N-1];
cosval[N-1]=1.0-sinval[N-1]*sinval[N-1]/2;
for(int i=N-2;i>=0;i--){
sinval[i]=2.0*sinval[i+1]*cosval[i+1];
cosval[i]=sqrt(1.0-sinval[i]*sinval[i]);
}
}
}
QuadReal_t t=(a<0.0?-a:a);
QuadReal_t sval=0.0;
QuadReal_t cval=1.0;
for(int i=0;i<N;i++){
while(theta[i]<=t){
QuadReal_t sval_=sval*cosval[i]+cval*sinval[i];
QuadReal_t cval_=cval*cosval[i]-sval*sinval[i];
sval=sval_;
cval=cval_;
t=t-theta[i];
}
}
return (a<0.0?-sval:sval);
}
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-12-14 00:19:31
Powiem inaczej, że pomysł ten pochodzi z przybliżenia funkcji cosinusowych i sinusoidalnych na przedziale [- pi/4,+pi / 4] z ograniczonym błędem przy użyciu algorytmu Remeza. Następnie, używając zredukowanej zmiennoprzecinkowej reszty zakresu i LUT dla wyjść cos & sinus ilorazu całkowitego, przybliżenie może być przeniesione do dowolnego argumentu kątowego.
Jest po prostu wyjątkowy i pomyślałem, że można go rozszerzyć, aby stworzyć bardziej wydajny algorytm pod względem ograniczonego błędu.
void sincos_fast(float x, float *pS, float *pC){
float cosOff4LUT[] = { 0x1.000000p+00, 0x1.6A09E6p-01, 0x0.000000p+00, -0x1.6A09E6p-01, -0x1.000000p+00, -0x1.6A09E6p-01, 0x0.000000p+00, 0x1.6A09E6p-01 };
int m, ms, mc;
float xI, xR, xR2;
float c, s, cy, sy;
// Cody & Waite's range reduction Algorithm, [-pi/4, pi/4]
xI = floorf(x * 0x1.45F306p+00 + 0.5); // This is 4/pi.
xR = (x - xI * 0x1.920000p-01) - xI*0x1.FB5444p-13; // This is pi/4 in two parts per C&W.
m = (int) xI;
xR2 = xR*xR;
// Find cosine & sine index for angle offsets indices
mc = ( m ) & 0x7; // two's complement permits upper modulus for negative numbers =P
ms = (m + 6) & 0x7; // phase correction for sine.
// Find cosine & sine
cy = cosOff4LUT[mc]; // Load angle offset neighborhood cosine value
sy = cosOff4LUT[ms]; // Load angle offset neighborhood sine value
c = 0xf.ff79fp-4 + xR2 * (-0x7.e58e9p-4); // TOL = 1.2786e-4
// c = 0xf.ffffdp-4 + xR2 * (-0x7.ffebep-4 + xR2 * 0xa.956a9p-8); // TOL = 1.7882e-7
s = xR * (0xf.ffbf7p-4 + xR2 * (-0x2.a41d0cp-4)); // TOL = 4.835251e-6
// s = xR * (0xf.fffffp-4 + xR2 * (-0x2.aaa65cp-4 + xR2 * 0x2.1ea25p-8)); // TOL = 1.1841e-8
*pC = c*cy - s*sy;
*pS = c*sy + s*cy;
}
float sqrt_fast(float x){
union {float f; int i; } X, Y;
float ScOff;
uint8_t e;
X.f = x;
e = (X.i >> 23); // f.SFPbits.e;
if(x <= 0) return(0.0f);
ScOff = ((e & 1) != 0) ? 1.0f : 0x1.6a09e6p0; // NOTE: If exp=EVEN, b/c (exp-127) a (EVEN - ODD) := ODD; but a (ODD - ODD) := EVEN!!
e = ((e + 127) >> 1); // NOTE: If exp=ODD, b/c (exp-127) then flr((exp-127)/2)
X.i = (X.i & ((1uL << 23) - 1)) | (0x7F << 23); // Mask mantissa, force exponent to zero.
Y.i = (((uint32_t) e) << 23);
// Error grows with square root of the exponent. Unfortunately no work around like inverse square root... :(
// Y.f *= ScOff * (0x9.5f61ap-4 + X.f*(0x6.a09e68p-4)); // Error = +-1.78e-2 * 2^(flr(log2(x)/2))
// Y.f *= ScOff * (0x7.2181d8p-4 + X.f*(0xa.05406p-4 + X.f*(-0x1.23a14cp-4))); // Error = +-7.64e-5 * 2^(flr(log2(x)/2))
// Y.f *= ScOff * (0x5.f10e7p-4 + X.f*(0xc.8f2p-4 +X.f*(-0x2.e41a4cp-4 + X.f*(0x6.441e6p-8)))); // Error = 8.21e-5 * 2^(flr(log2(x)/2))
// Y.f *= ScOff * (0x5.32eb88p-4 + X.f*(0xe.abbf5p-4 + X.f*(-0x5.18ee2p-4 + X.f*(0x1.655efp-4 + X.f*(-0x2.b11518p-8))))); // Error = +-9.92e-6 * 2^(flr(log2(x)/2))
// Y.f *= ScOff * (0x4.adde5p-4 + X.f*(0x1.08448cp0 + X.f*(-0x7.ae1248p-4 + X.f*(0x3.2cf7a8p-4 + X.f*(-0xc.5c1e2p-8 + X.f*(0x1.4b6dp-8)))))); // Error = +-1.38e-6 * 2^(flr(log2(x)/2))
// Y.f *= ScOff * (0x4.4a17fp-4 + X.f*(0x1.22d44p0 + X.f*(-0xa.972e8p-4 + X.f*(0x5.dd53fp-4 + X.f*(-0x2.273c08p-4 + X.f*(0x7.466cb8p-8 + X.f*(-0xa.ac00ep-12))))))); // Error = +-2.9e-7 * 2^(flr(log2(x)/2))
Y.f *= ScOff * (0x3.fbb3e8p-4 + X.f*(0x1.3b2a3cp0 + X.f*(-0xd.cbb39p-4 + X.f*(0x9.9444ep-4 + X.f*(-0x4.b5ea38p-4 + X.f*(0x1.802f9ep-4 + X.f*(-0x4.6f0adp-8 + X.f*(0x5.c24a28p-12 )))))))); // Error = +-2.7e-6 * 2^(flr(log2(x)/2))
return(Y.f);
}
The dłuższe wyrażenia są dłuższe, wolniejsze, ale bardziej precyzyjne. Wielomiany zapisywane są według reguły Hornera .
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-12-16 00:09:32
Jest to implementacja sinus, która powinna być dość szybka, działa tak:
Ma arytmetyczną implementację kwadratowej liczby zespolonej
Z analizy matematycznej z liczbami zespolonymi wiadomo, że kąt jest połowiczny, gdy liczba zespolona jest kwadratowa
Możesz wziąć liczbę zespoloną, której kąt już znasz (np. i, ma kąt 90 stopni lub radiany PI / 2)
Niż przez ukorzenienie kwadratowe można uzyskać liczby zespolone postaci cos (90 / 2^n) + i sin (90 / 2^n)
Z analizy matematycznej z liczbami zespolonymi wiadomo, że gdy dwie liczby mnożą ich kąty sumują się
Możesz pokazać liczbę k (którą otrzymujesz jako argument w sin lub cos) jako sumę kątów 90 / 2^n, a następnie uzyskać wartości wynikowe, mnożąc te liczby złożone, które wcześniej obliczyłeś
Wynik będzie w postaci cos K + i sin k
#define PI 3.14159265
#define complex pair <float, float>
/* this is square root function, uses binary search and halves mantisa */
float sqrt(float a) {
float b = a;
int *x = (int*) (&b); // here I get integer pointer to float b which allows me to directly change bits from float reperesentation
int c = ((*x >> 23) & 255) - 127; // here I get mantisa, that is exponent of 2 (floats are like scientific notation 1.111010101... * 2^n)
if(c < 0) c = -((-c) >> 1); // ---
// |--> This is for halfing the mantisa
else c >>= 1; // ---
*x &= ~(255 << 23); // here space reserved for mantisa is filled with 0s
*x |= (c + 127) << 23; // here new mantisa is put in place
for(int i = 0; i < 5; i++) b = (b + a / b) / 2; // here normal square root approximation runs 5 times (I assume even 2 or 3 would be enough)
return b;
}
/* this is a square root for complex numbers (I derived it in paper), you'll need it later */
complex croot(complex x) {
float c = x.first, d = x.second;
return make_pair(sqrt((c + sqrt(c * c + d * d)) / 2), sqrt((-c + sqrt(c * c + d * d)) / 2) * (d < 0 ? -1 : 1));
}
/* this is for multiplying complex numbers, you'll also need it later */
complex mul(complex x, complex y) {
float a = x.first, b = x.second, c = y.first, d = y.second;
return make_pair(a * c - b * d, a * d + b * c);
}
/* this function calculates both sinus and cosinus */
complex roots[24];
float angles[24];
void init() {
complex c = make_pair(-1, 0); // first number is going to be -1
float alpha = PI; // angle of -1 is PI
for(int i = 0; i < 24; i++) {
roots[i] = c; // save current c
angles[i] = alpha; // save current angle
c = croot(c); // root c
alpha *= 0.5; // halve alpha
}
}
complex cosin(float k) {
complex r = make_pair(1, 0); // at start 1
for(int i = 0; i < 24; i++) {
if(k >= angles[i]) { // if current k is bigger than angle of c
k -= angles[i]; // reduce k by that number
r = mul(r, roots[i]); // multiply the result by c
}
}
return r; // here you'll have a complex number equal to cos k + i sin k.
}
float sin(float k) {
return cosin(k).second;
}
float cos(float k) {
return cosin(k).first;
}
Teraz, jeśli nadal będzie to wolne, możesz zmniejszyć liczbę iteracji w funkcji cosin (zauważ, że precision will be reduced)
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-04-16 23:45:59
Przybliżenie funkcji sinusoidalnej, która zachowuje pochodne w wielokrotnościach 90 stopni, jest podane przez Ten wzór . Pochodna jest podobna do Bhaskara I ' S sinus aproksymacji Formuły , ale ograniczenia są ustawić wartości i pochodne na 0, 90 i 180 stopni do funkcji sinus. Możesz tego użyć, jeśli chcesz, aby funkcja była płynna wszędzie.
#define PI 3.141592653589793
double fast_sin(double x) {
x /= 2 * PI;
x -= (int) x;
if (x <= 0.5) {
double t = 2 * x * (2 * x - 1);
return (PI * t) / ((PI - 4) * t - 1);
}
else {
double t = 2 * (1 - x) * (1 - 2 * x);
return -(PI * t) / ((PI - 4) * t - 1);
}
}
double fast_cos(double x) {
return fast_sin(x + 0.5 * PI);
}
Jeśli chodzi o prędkość, to przynajmniej przewyższa funkcję std::sin() średnio o 0,3 mikrosekundy na połączenie. A maksymalny błąd absolutny wynosi 0,0051.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-06-17 09:04:03
Jest to implementacja metody szeregów Taylora podanej wcześniej w odpowiedzi akellehe ' a.
unsigned int Math::SIN_LOOP = 15;
unsigned int Math::COS_LOOP = 15;
// sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
template <class T>
T Math::sin(T x)
{
T Sum = 0;
T Power = x;
T Sign = 1;
const T x2 = x * x;
T Fact = 1.0;
for (unsigned int i=1; i<SIN_LOOP; i+=2)
{
Sum += Sign * Power / Fact;
Power *= x2;
Fact *= (i + 1) * (i + 2);
Sign *= -1.0;
}
return Sum;
}
// cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
template <class T>
T Math::cos(T x)
{
T Sum = x;
T Power = x;
T Sign = 1.0;
const T x2 = x * x;
T Fact = 1.0;
for (unsigned int i=3; i<COS_LOOP; i+=2)
{
Power *= x2;
Fact *= i * (i - 1);
Sign *= -1.0;
Sum += Sign * Power / Fact;
}
return Sum;
}
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-05-23 12:26:32
Po prostu użyj FPU z wbudowanym x86 dla aplikacji Wintel. Funkcja direct CPU sqrt jest podobno nadal bije wszelkie inne algorytmy w szybkości. Mój niestandardowy kod biblioteki Matematycznej x86 jest dla standardowego MSVC++ 2005 i forward. Potrzebujesz osobnych wersji float/double, jeśli chcesz więcej precyzji, którą pokryłem. Czasami strategia kompilatora "_ _ inline " idzie źle, więc dla bezpieczeństwa można ją usunąć. Dzięki doświadczeniu możesz przełączyć się na makra, aby całkowicie uniknąć wywołania funkcji za każdym razem.
extern __inline float __fastcall fs_sin(float x);
extern __inline double __fastcall fs_Sin(double x);
extern __inline float __fastcall fs_cos(float x);
extern __inline double __fastcall fs_Cos(double x);
extern __inline float __fastcall fs_atan(float x);
extern __inline double __fastcall fs_Atan(double x);
extern __inline float __fastcall fs_sqrt(float x);
extern __inline double __fastcall fs_Sqrt(double x);
extern __inline float __fastcall fs_log(float x);
extern __inline double __fastcall fs_Log(double x);
extern __inline float __fastcall fs_sqrt(float x) { __asm {
FLD x ;// Load/Push input value
FSQRT
}}
extern __inline double __fastcall fs_Sqrt(double x) { __asm {
FLD x ;// Load/Push input value
FSQRT
}}
extern __inline float __fastcall fs_sin(float x) { __asm {
FLD x ;// Load/Push input value
FSIN
}}
extern __inline double __fastcall fs_Sin(double x) { __asm {
FLD x ;// Load/Push input value
FSIN
}}
extern __inline float __fastcall fs_cos(float x) { __asm {
FLD x ;// Load/Push input value
FCOS
}}
extern __inline double __fastcall fs_Cos(double x) { __asm {
FLD x ;// Load/Push input value
FCOS
}}
extern __inline float __fastcall fs_tan(float x) { __asm {
FLD x ;// Load/Push input value
FPTAN
}}
extern __inline double __fastcall fs_Tan(double x) { __asm {
FLD x ;// Load/Push input value
FPTAN
}}
extern __inline float __fastcall fs_log(float x) { __asm {
FLDLN2
FLD x
FYL2X
FSTP ST(1) ;// Pop1, Pop2 occurs on return
}}
extern __inline double __fastcall fs_Log(double x) { __asm {
FLDLN2
FLD x
FYL2X
FSTP ST(1) ;// Pop1, Pop2 occurs on return
}}
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-07-25 19:13:37
Oto możliwe przyspieszenie, które zależy w dużej mierze od twojej aplikacji. (Twój program może nie być w stanie tego w ogóle użyć, ale zamieszczam go tutaj, ponieważ może.) Zamieszczam też tutaj matematykę, kod zależy od Ciebie.
Do mojego zastosowania, musiałem obliczyć sinusy i cosines dla każdego kroku kątowego (dA) wokół pełnego okręgu.
To sprawiło, że mogłem skorzystać z niektórych Trig:
Cos (- A) = cos(a)
Sin (- A) = - sin (a)
This made it więc musiałem tylko obliczyć sin i cos dla jednej połowy okręgu.
Ustawiłem również wskaźniki do tablic wyjściowych, co przyspieszyło moje obliczenia. Nie jestem tego pewien, ale wierzę, że mój kompilator wektoryzował moje obliczenia.
Trzeci był do użycia:
Sin (a+dA) = sin(a) * cos(dA) + cos (a) * sin (dA)
Cos(a+dA) = cos(A)*cos(dA) - sin(a) * sin (dA)
To sprawiło, że musiałem tylko faktycznie obliczyć grzech i cos z jednego kąta - reszta została obliczona z dwoma mnożnikami i dodawaniem. (Chodzi o zastrzeżenie, że błędy zaokrąglania w obliczeniach sin (dA) i cos (dA) mogą kumulować się do czasu, gdy uzyskasz połowę okrążenia okręgu. Po raz kolejny, Twoja aplikacja jest wszystkim, jeśli tego użyjesz.)
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-12-08 17:42:12
Ponad 1000000000 test, odpowiedź milianw jest 2 razy wolniejsza niż implementacja std:: cos. Możesz jednak uruchomić go szybciej, wykonując następujące kroki:
- > Użyj float
- >nie używaj floor ale static_cast
- >nie używaj abs, ale trójwarstwowego warunkowego
- > Użyj # define stałej dla podziału
- > Użyj makra, aby uniknąć wywołania funkcji
// 1 / (2 * PI)
#define FPII 0.159154943091895
//PI / 2
#define PI2 1.570796326794896619
#define _cos(x) x *= FPII;\
x -= .25f + static_cast<int>(x + .25f) - 1;\
x *= 16.f * ((x >= 0 ? x : -x) - .5f);
#define _sin(x) x -= PI2; _cos(x);
Ponad 100000000 wywołanie std:: cos I _cos (x), STD:: cos uruchom na ~14s vs ~3s dla _cos (x) (trochę więcej dla _sin (x))
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2016-05-11 07:26:11