Zrozumienie einsum NumPy ' ego
Ciężko mi zrozumieć, jak dokładnie działa. Przejrzałem dokumentację i kilka przykładów, ale nie wydaje się, aby trzymać.
Oto przykład, który przejrzeliśmy w klasie:
C = np.einsum("ij,jk->ki", A, B)
Dla dwóch tablic A i B
Myślę, że to zajmie A^T * B, ale nie jestem pewien (chodzi o transpozycję jednego z nich, prawda?). Czy ktoś może mi opowiedzieć dokładnie o tym ,co się tutaj dzieje (i w ogóle podczas używania einsum)?
7 answers
(Uwaga: Ta odpowiedź jest oparta na krótkim blogu o einsum napisałem jakiś czas temu.)
Co robi einsum?
Wyobraź sobie, że mamy dwie wielowymiarowe tablice, A i B. Załóżmy, że chcemy...
-
mnożenie
AzBw szczególny sposób do tworzenia nowej tablicy produktów; a następnie może - suma ta nowa tablica wzdłuż poszczególnych osi; a potem może
- transpozycja osie nowej tablicy w określonej kolejności.
Istnieje duża szansa, że einsum pomoże nam to zrobić szybciej i wydajniej, że kombinacje funkcji NumPy jak multiply, sum i transpose pozwoli.
Jak działa einsum?
Oto prosty (ale nie do końca trywialny) przykład. Weź następujące dwie tablice:
A = np.array([0, 1, 2])
B = np.array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
Będziemy mnożyć A i B elementowo, a następnie zsumować wzdłuż wierszy nowej tablicy. W "normal" NumPy piszemy:
>>> (A[:, np.newaxis] * B).sum(axis=1)
array([ 0, 22, 76])
Więc tutaj, operacja indeksowania na A ustawia pierwsze osie dwóch tablic tak, że mnożenie może być transmitowane. Wiersze tablicy produktów są następnie sumowane, aby zwrócić odpowiedź.
Teraz, gdybyśmy chcieli użyć einsum zamiast tego, moglibyśmy napisać:
>>> np.einsum('i,ij->i', A, B)
array([ 0, 22, 76])
The signature string 'i,ij->i' jest tutaj kluczem i wymaga trochę wyjaśnienia. Możesz myśleć o tym w dwóch połówkach. Po lewej stronie (po lewej ->) oznaczyliśmy dwie tablice wejściowe. Po prawej stronie ->, oznaczyliśmy tablicę, z którą chcemy skończyć.
Oto co będzie dalej:
Aposiada jedną oś; oznaczamy jąi. IBma dwie osie; oznaczamy oś 0 jakoi, a oś 1 jakoj.Przez powtórzenie etykiety
iw obu tablicach wejściowych mówimyeinsum, że te dwie osie powinny być pomnożone razem. W innymi słowy, mnożymy tablicęAz każdą kolumną tablicyB, tak jak robi toA[:, np.newaxis] * B.Zauważ, że
jnie pojawia się jako etykieta w naszym żądanym wyjściu; właśnie użyliśmyi(chcemy skończyć z tablicą 1D). Przez pominięcie etykiety, mówimyeinsumdo sumy wzdłuż tej osi. Innymi słowy, sumujemy rzędy produktów, tak jak robi to.sum(axis=1).
To w zasadzie wszystko, co musisz wiedzieć, aby użyj einsum. Pomaga to trochę grać; jeśli zostawimy obie etykiety w wyjściu, 'i,ij->ij', otrzymamy z powrotem tablicę produktów 2D(taką samą jak A[:, np.newaxis] * B). Jeśli powiemy brak etykiet wyjściowych, 'i,ij->, otrzymamy z powrotem pojedynczy numer(tak samo jak w przypadku (A[:, np.newaxis] * B).sum()).
Wspaniałą rzeczą w einsum jest jednak to, że nie buduje najpierw tymczasowej tablicy produktów; po prostu sumuje produkty tak, jak idzie. Może to prowadzić do dużych oszczędności w użyciu pamięci.
Nieco większy przykład
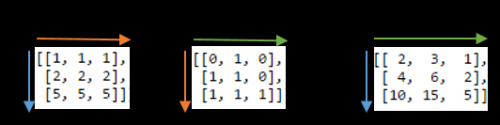
Aby wyjaśnić produkt dot, oto dwie nowe tablice:
A = array([[1, 1, 1],
[2, 2, 2],
[5, 5, 5]])
B = array([[0, 1, 0],
[1, 1, 0],
[1, 1, 1]])
Obliczymy iloczyn kropkowy używając np.einsum('ij,jk->ik', A, B). Oto zdjęcie pokazujące etykietowanie A i B oraz macierz wyjściową, którą otrzymujemy z funkcji:
Widać, że etykieta j jest powtarzana - oznacza to, że mnożymy wiersze {[13] } z kolumnami B. Co więcej, Etykieta j nie jest zawarta w produkcie wyjściowym - podsumowujemy te produkty. Etykiety i i k są przechowywane dla wyjścia, więc otrzymujemy tablicę 2D.
Może być jeszcze jaśniejsze porównanie tego wyniku z tablicą, w której Etykieta jjest , a nie sumowana. Poniżej, po lewej stronie widać tablicę 3D wynikającą z zapisu np.einsum('ij,jk->ijk', A, B) (tzn. zachowaliśmy Etykietę j):
Oś sumująca j daje oczekiwany iloczyn punktowy, pokazany po prawej stronie.
Niektóre ćwiczenia
Aby uzyskać więcej wyczucia dla einsum, można przydatne do implementacji znanych operacji tablic NumPy przy użyciu notacji dolnej. Wszystko, co wiąże się z kombinacjami mnożenia i sumowania osi, można zapisać za pomocą einsum.
Niech A i B będą dwiema tablicami 1D o tej samej długości. Na przykład, A = np.arange(10) i B = np.arange(5, 15).
-
Sumę
Amożna zapisać:np.einsum('i->', A) -
Mnożenie pierwiastków,
A * B, można zapisać:np.einsum('i,i->i', A, B) -
Produkt wewnętrzny lub produkt kropkowy,
np.inner(A, B)lubnp.dot(A, B), można zapisać:np.einsum('i,i->', A, B) # or just use 'i,i' -
Iloczyn zewnętrzny,
np.outer(A, B), można zapisać:np.einsum('i,j->ij', A, B)
Dla tablic 2D, C i D, pod warunkiem, że osie są zgodnymi długościami (zarówno tej samej długości, jak i jednej z nich o długości 1), Oto kilka przykładów:
-
Ślad
C(suma przekątnej głównej),np.trace(C), można zapisać:np.einsum('ii', C) -
Mnożenie pierwiastków
Ci transpozycjaD,C * D.T, można zapisać:np.einsum('ij,ji->ij', C, D) -
Mnożenie każdego elementu
Cprzez tablicęD(aby utworzyć tablicę 4D),C[:, :, None, None] * D, można zapisać:np.einsum('ij,kl->ijkl', C, D)
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2018-01-12 20:50:40
Uchwycenie idei numpy.einsum() jest to bardzo proste, jeśli rozumiesz to intuicyjnie. Jako przykład, zacznijmy od prostego opisu obejmującego mnożenie macierzy.
Aby użyć numpy.einsum(), wszystko, co musisz zrobić, to przekazać tak zwany łańcuch indeksu jako argument, a następnie tablice wejściowe.
Powiedzmy, że masz dwie tablice 2D, A oraz B, i chcesz do mnożenia macierzy. Więc robisz:
np.einsum("ij, jk -> ik", A, B)
Tutaj łańcuch dolny ij odpowiada tablicy A podczas gdy łańcuch dolny jk odpowiada tablicy B. Ponadto, najważniejszą rzeczą do odnotowania tutaj jest to, że liczba znaków w każdym łańcuchu dolnym musi dopasować wymiary tablicy. (tj. dwa znaki dla tablic 2D, trzy znaki dla tablic 3D, a więc on) I jeśli powtórzysz znaki pomiędzy łańcuchami (j w naszym przypadku), to oznacza, że chcesz einsum do zaistnienia wzdłuż tych wymiarów. W ten sposób zostaną one zredukowane. (tzn. wymiar ten będzie zniknął )
łańcuch dolny Po tym ->, będzie naszym wynikowym układem.
Jeśli pozostawisz go pusty, wtedy wszystko zostanie zsumowane i wartość skalarna zostanie zwrócona jako wynik. Else tablica wynikowa będzie miał wymiary zgodne z łańcuchem dolnym . W naszym przykładzie będzie to ik. Jest to intuicyjne, ponieważ wiemy, że dla mnożenia macierzy liczba kolumn w tablicy A musi pasować do liczby wierszy w tablicy B co się tutaj dzieje (tj. zakodujemy tę wiedzę powtarzając znak j in the subscript string )
Oto kilka przykładów ilustrujących zastosowanie / moc np.einsum() w implementacji pewnych typowych operacji tensor lub ND-array , zwięźle.
Wejścia
# a vector
In [197]: vec
Out[197]: array([0, 1, 2, 3])
# an array
In [198]: A
Out[198]:
array([[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34],
[41, 42, 43, 44]])
# another array
In [199]: B
Out[199]:
array([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]])
1) mnożenie macierzy (podobne do np.matmul(arr1, arr2))
In [200]: np.einsum("ij, jk -> ik", A, B)
Out[200]:
array([[130, 130, 130, 130],
[230, 230, 230, 230],
[330, 330, 330, 330],
[430, 430, 430, 430]])
2) wyodrębnić elementy wzdłuż głównej przekątnej (podobnie jak np.diag(arr))
In [202]: np.einsum("ii -> i", A)
Out[202]: array([11, 22, 33, 44])
3) iloczyn Hadamarda (tzn. iloczyn elementów dwóch tablic) (podobny do arr1 * arr2)
In [203]: np.einsum("ij, ij -> ij", A, B)
Out[203]:
array([[ 11, 12, 13, 14],
[ 42, 44, 46, 48],
[ 93, 96, 99, 102],
[164, 168, 172, 176]])
4) Element-wise squaring (podobne do np.square(arr) lub arr ** 2)
In [210]: np.einsum("ij, ij -> ij", B, B)
Out[210]:
array([[ 1, 1, 1, 1],
[ 4, 4, 4, 4],
[ 9, 9, 9, 9],
[16, 16, 16, 16]])
5) Trace (tj. suma elementów main-diagonal) (podobnie jak np.trace(arr))
In [217]: np.einsum("ii -> ", A)
Out[217]: 110
6) Transpozycja matrycy (podobna do np.transpose(arr))
In [221]: np.einsum("ij -> ji", A)
Out[221]:
array([[11, 21, 31, 41],
[12, 22, 32, 42],
[13, 23, 33, 43],
[14, 24, 34, 44]])
7) iloczyn zewnętrzny (wektorów) (podobny do np.outer(vec1, vec2))
In [255]: np.einsum("i, j -> ij", vec, vec)
Out[255]:
array([[0, 0, 0, 0],
[0, 1, 2, 3],
[0, 2, 4, 6],
[0, 3, 6, 9]])
8) iloczyn wewnętrzny (wektorów) (podobny do np.inner(vec1, vec2))
In [256]: np.einsum("i, i -> ", vec, vec)
Out[256]: 14
9) suma wzdłuż osi 0 (podobna do np.sum(arr, axis=0))
In [260]: np.einsum("ij -> j", B)
Out[260]: array([10, 10, 10, 10])
10) suma wzdłuż osi 1 (podobna do np.sum(arr, axis=1))
In [261]: np.einsum("ij -> i", B)
Out[261]: array([ 4, 8, 12, 16])
11) Mnożenie Macierzy Wsadowych
In [287]: BM = np.stack((A, B), axis=0)
In [288]: BM
Out[288]:
array([[[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34],
[41, 42, 43, 44]],
[[ 1, 1, 1, 1],
[ 2, 2, 2, 2],
[ 3, 3, 3, 3],
[ 4, 4, 4, 4]]])
In [289]: BM.shape
Out[289]: (2, 4, 4)
# batch matrix multiply using einsum
In [292]: BMM = np.einsum("bij, bjk -> bik", BM, BM)
In [293]: BMM
Out[293]:
array([[[1350, 1400, 1450, 1500],
[2390, 2480, 2570, 2660],
[3430, 3560, 3690, 3820],
[4470, 4640, 4810, 4980]],
[[ 10, 10, 10, 10],
[ 20, 20, 20, 20],
[ 30, 30, 30, 30],
[ 40, 40, 40, 40]]])
In [294]: BMM.shape
Out[294]: (2, 4, 4)
12) suma wzdłuż osi 2 (podobna do np.sum(arr, axis=2))
In [330]: np.einsum("ijk -> ij", BM)
Out[330]:
array([[ 50, 90, 130, 170],
[ 4, 8, 12, 16]])
13) sumuje wszystkie elementy w tablicy (podobnie jak np.sum(arr))
In [335]: np.einsum("ijk -> ", BM)
Out[335]: 480
14) suma na wielu osiach (tj. marginalizacja)
(podobne do np.sum(arr, axis=(axis0, axis1, axis2, axis3, axis4, axis6, axis7)))
# 8D array
In [354]: R = np.random.standard_normal((3,5,4,6,8,2,7,9))
# marginalize out axis 5 (i.e. "n" here)
In [363]: esum = np.einsum("ijklmnop -> n", R)
# marginalize out axis 5 (i.e. sum over rest of the axes)
In [364]: nsum = np.sum(R, axis=(0,1,2,3,4,6,7))
In [365]: np.allclose(esum, nsum)
Out[365]: True
15) produkty Double Dot (podobne do np.suma (produkt hadamarda) por. 3)
In [772]: A
Out[772]:
array([[1, 2, 3],
[4, 2, 2],
[2, 3, 4]])
In [773]: B
Out[773]:
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
In [774]: np.einsum("ij, ij -> ", A, B)
Out[774]: 124
16) mnożenie tablic 2D i 3D
Takie mnożenie może być bardzo przydatne przy rozwiązywaniu liniowego układu równań (Ax = b), gdzie chcemy zweryfikować wynik.
# inputs
In [115]: A = np.random.rand(3,3)
In [116]: b = np.random.rand(3, 4, 5)
# solve for x
In [117]: x = np.linalg.solve(A, b.reshape(b.shape[0], -1)).reshape(b.shape)
# 2D and 3D array multiplication :)
In [118]: Ax = np.einsum('ij, jkl', A, x)
# indeed the same!
In [119]: np.allclose(Ax, b)
Out[119]: True
Wręcz przeciwnie, jeśli trzeba użyć np.matmul() W przypadku tej weryfikacji musimy wykonać kilka operacji reshape, aby osiągnąć ten sam wynik, jak:
# reshape 3D array `x` to 2D, perform matmul
# then reshape the resultant array to 3D
In [123]: Ax_matmul = np.matmul(A, x.reshape(x.shape[0], -1)).reshape(x.shape)
# indeed correct!
In [124]: np.allclose(Ax, Ax_matmul)
Out[124]: True
Bonus : Czytaj więcej matematyki tutaj : Einstein-sumowanie i zdecydowanie tutaj: Tensor-notacja
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-10-06 05:15:44
Pozwala utworzyć 2 tablice, o różnych, ale kompatybilnych wymiarach, aby podkreślić ich wzajemne oddziaływanie
In [43]: A=np.arange(6).reshape(2,3)
Out[43]:
array([[0, 1, 2],
[3, 4, 5]])
In [44]: B=np.arange(12).reshape(3,4)
Out[44]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
Twoje obliczenie, bierze "kropkę" (sumę produktów) z (2,3) z (3,4) do wytworzenia tablicy (4,2). i jest pierwszym dim z A, ostatnim z C; k Ostatni z B, pierwszy z C. j jest "konsumowane" przez sumowanie.
In [45]: C=np.einsum('ij,jk->ki',A,B)
Out[45]:
array([[20, 56],
[23, 68],
[26, 80],
[29, 92]])
To jest to samo co np.dot(A,B).T - to końcowe wyjście jest transponowane.
Aby zobaczyć więcej tego, co dzieje się z j, Zmień C indeks dolny do ijk:
In [46]: np.einsum('ij,jk->ijk',A,B)
Out[46]:
array([[[ 0, 0, 0, 0],
[ 4, 5, 6, 7],
[16, 18, 20, 22]],
[[ 0, 3, 6, 9],
[16, 20, 24, 28],
[40, 45, 50, 55]]])
To może być również produkowane z:
A[:,:,None]*B[None,:,:]
To znaczy, dodać k Wymiar na końcu A i i na początku B, co daje tablicę (2,3,4).
0 + 4 + 16 = 20, 9 + 28 + 55 = 92, etc; suma na j i transponować, aby uzyskać wcześniejszy wynik:
np.sum(A[:,:,None] * B[None,:,:], axis=1).T
# C[k,i] = sum(j) A[i,j (,k) ] * B[(i,) j,k]
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2014-09-29 22:25:10
Znalazłem NumPy: sztuczki handlu (Część II) pouczające
Używamy -> do wskazania kolejności wyjściowej tablicy. Pomyśl więc o 'ij, i - > j' jako o lewej stronie (LHS) i prawej stronie (RHS). Każde powtórzenie etykiet na LHS oblicza element produktu wise, a następnie sumuje. Zmieniając etykietę po stronie RHS (output) możemy zdefiniować oś, w której chcemy postępować względem tablicy wejściowej, czyli sumowanie wzdłuż osi 0, 1 i tak on
import numpy as np
>>> a
array([[1, 1, 1],
[2, 2, 2],
[3, 3, 3]])
>>> b
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> d = np.einsum('ij, jk->ki', a, b)
Zauważ, że są trzy osie, i, j, k, i że J jest powtarzane (po lewej stronie). i,j reprezentują wiersze i kolumny dla a. j,k dla b.
Aby obliczyć iloczyn i wyrównać oś j musimy dodać oś do a. (b będzie transmitowane wzdłuż (?) pierwsza oś)
a[i, j, k]
b[j, k]
>>> c = a[:,:,np.newaxis] * b
>>> c
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]],
[[ 0, 3, 6],
[ 9, 12, 15],
[18, 21, 24]]])
j jest nieobecny z prawej strony, więc sumujemy j, która jest drugą osią tablicy 3x3x3
>>> c = c.sum(1)
>>> c
array([[ 9, 12, 15],
[18, 24, 30],
[27, 36, 45]])
Wreszcie, indeksy są (Alfabetycznie) odwrócone po prawej stronie, więc transponujemy.
>>> c.T
array([[ 9, 18, 27],
[12, 24, 36],
[15, 30, 45]])
>>> np.einsum('ij, jk->ki', a, b)
array([[ 9, 18, 27],
[12, 24, 36],
[15, 30, 45]])
>>>
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-11-24 07:02:12
Podczas czytania równań einsuma, uznałem, że najbardziej pomocne jest po prostu umieć mentalnie sprowadzają je do ich imperatywnych wersji.
Zacznijmy od następującego (narzucającego) stwierdzenia:
C = np.einsum('bhwi,bhwj->bij', A, B)
Pracując nad interpunkcją najpierw widzimy, że mamy dwa 4-literowe bloby oddzielone przecinkami-bhwi i bhwj, przed strzałką,
i jedna 3-literowa blob bij po niej. Dlatego równanie daje wynik tensora rangi-3 z dwóch tensorów rangi-4 wejścia.
Niech każda litera w każdej blob będzie nazwą zmiennej range. Pozycja, w której litera pojawia się w blob jest indeksem osi, nad którą się mieści w tym tensorze. W tym celu należy utworzyć trzy zagnieżdżone pętle, po jednej dla każdego indeksu C.]}
for b in range(...):
for i in range(...):
for j in range(...):
# the variables b, i and j index C in the order of their appearance in the equation
C[b, i, j] = ...
Więc, zasadniczo, masz pętlę for dla każdego indeksu wyjściowego C. na razie pozostawimy zakresy nieokreślone.
Następnie szukamy po lewej stronie - czy są tam jakieś zmienne zakresowe, które nie pojawiają siępo prawej stronie ? W naszym przypadku-tak, h i w.
Dodaj wewnętrzną zagnieżdżoną pętlę for dla każdej takiej zmiennej:
for b in range(...):
for i in range(...):
for j in range(...):
C[b, i, j] = 0
for h in range(...):
for w in range(...):
...
Wewnątrz pętli wewnętrznej mamy teraz zdefiniowane wszystkie indeksy, więc możemy zapisać rzeczywiste podsumowanie i tłumaczenie jest kompletne:
# three nested for-loops that index the elements of C
for b in range(...):
for i in range(...):
for j in range(...):
# prepare to sum
C[b, i, j] = 0
# two nested for-loops for the two indexes that don't appear on the right-hand side
for h in range(...):
for w in range(...):
# Sum! Compare the statement below with the original einsum formula
# 'bhwi,bhwj->bij'
C[b, i, j] += A[b, h, w, i] * B[b, h, w, j]
Jeśli udało Ci się do tej pory przestrzegać kodu, to gratulacje! To wszystko, czego potrzebujesz, aby móc czytać równania einsum. Zwróć uwagę w szczególności na to, jak oryginalna formuła einsum odwzorowuje ostateczne podsumowanie w powyższym fragmencie. Pętle for i granice zasięgu są po prostu puszyste, a to ostateczne stwierdzenie jest wszystkim, czego naprawdę potrzebujesz, aby zrozumieć, o co chodzi.
Ze względu na kompletność, zobaczmy, jak określić zakresy dla każdej zmiennej zakresu. Cóż, zakres każdej zmiennej jest po prostu długością wymiaru(wymiarów), które indeksuje. Oczywiście, jeśli zmienna indeksuje więcej niż jeden wymiar w jednym lub kilku tensorach, wtedy długości każdego z tych wymiarów muszą być równe. Oto powyższy kod z pełnymi zakresami:
# C's shape is determined by the shapes of the inputs
# b indexes both A and B, so its range can come from either A.shape or B.shape
# i indexes only A, so its range can only come from A.shape, the same is true for j and B
assert A.shape[0] == B.shape[0]
assert A.shape[1] == B.shape[1]
assert A.shape[2] == B.shape[2]
C = np.zeros((A.shape[0], A.shape[3], B.shape[3]))
for b in range(A.shape[0]): # b indexes both A and B, or B.shape[0], which must be the same
for i in range(A.shape[3]):
for j in range(B.shape[3]):
# h and w can come from either A or B
for h in range(A.shape[1]):
for w in range(A.shape[2]):
C[b, i, j] += A[b, h, w, i] * B[b, h, w, j]
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-01-22 11:35:30
Kolejny widok na np.einsum
Większość odpowiedzi tutaj wyjaśnić na przykład, pomyślałem, że dam dodatkowy punkt widzenia.
np.einsum jest ogólnym narzędziem pracy matrycy. Podany łańcuch zawiera indeksy dolne, które są etykietami reprezentującymi osie. Lubię myśleć o tym jako o twojej operacji. Indeksy dolne zapewniają dwa widoczne ograniczenia:
-
Liczba osi dla każdej tablicy wejściowej,
-
Równość wielkości osi między wejścia.
Weźmy przykład początkowy: np.einsum('ij,jk->ki', A, B). Tutaj ograniczenia 1. tłumaczy się na A.ndim == 2 i B.ndim == 2 oraz2. do A.shape[1] == B.shape[0].
Jak zobaczysz później, istnieją inne ograniczenia. Na przykład:
-
Etykiety w indeksie wyjściowym nie mogą pojawić się więcej niż jeden raz.
-
Etykiety w indeksie wyjściowym muszą pojawić się w indeksie wejściowym.
Kiedy patrząc na ij,jk->ki, można o tym myśleć jako:
Które komponenty tablic wejściowych przyczynią się do komponentu
[k, i]tablicy wyjściowej .
Indeksy dolne zawierają dokładną definicję operacji dla każdego składnika tablicy wyjściowej.
Będziemy trzymać się operacji ij,jk->ki I następujących definicji A i B:
>>> A = np.array([[1,4,1,7], [8,1,2,2], [7,4,3,4]])
>>> A.shape
(3, 4)
>>> B = np.array([[2,5], [0,1], [5,7], [9,2]])
>>> B.shape
(4, 2)
Wyjście, Z, będzie miało kształt (B.shape[1], A.shape[0]) i może być skonstruowane w podążam za nim. Począwszy od pustej tablicy dla Z:
Z = np.zeros((B.shape[1], A.shape[0]))
for i in range(A.shape[0]):
for j in range(A.shape[1]):
for k range(B.shape[0]):
Z[k, i] += A[i, j]*B[j, k] # ki <- ij*jk
np.einsum polega na gromadzeniu wkładów w macierzy wyjściowej. Każda para (A[i,j], B[j,k]) jest postrzegana jako składowa składowa Z[k, i].
Być może zauważyłeś, że wygląda to bardzo podobnie do tego, jak byś poszedł o obliczaniu ogólnych mnożenia macierzy...
Minimalna implementacja
Oto, nieco, minimalna implementacja np.einsum w Pythonie. Dla niektórych może to pomóc w zrozumieniu co naprawdę dzieje się pod maską. Uważam, że jest tak intuicyjny, jak samo użycie np.einsum.
Idąc dalej będę odwoływał się do poprzedniego przykładu. I zdefiniuj inputs jako [A, B].
np.einsum może przyjąć więcej niż dwa wejścia! Poniżej skupimy się na ogólnym przypadku: N input I n input indeksy dolne. Głównym celem jest znalezienie domeny badania, tj. iloczyn kartezjański wszystkich możliwych przedziałów.
Nie możemy polegaj na ręcznym pisaniu for pętli, po prostu dlatego, że nie wiemy, ile będziemy potrzebować! Główną ideą jest to, że musimy znaleźć wszystkie unikalne etykiety( użyję key i keys, aby się do nich odnieść), znaleźć odpowiedni kształt tablicy, następnie utworzyć zakresy dla każdego z nich i obliczyć iloczyn zakresów za pomocą itertools.product aby uzyskać domenę ucz się.
| indeks | keys |
ograniczenia | sizes |
ranges |
|---|---|---|---|---|
| 1 | 'i' |
A.shape[0] |
3 | range(0, 3) |
| 2 | 'j' |
A.shape[1] == B.shape[0] |
4 | range(0, 4) |
| 0 | 'k' |
B.shape[1] |
2 | range(0, 2) |
The dziedziną badań jest iloczyn kartezjański: range(0, 2) x range(0, 3) x range(0, 4).
-
Przetwarzanie indeksów dolnych:
>>> expr = 'ij,jk->ki' >>> qry_expr, res_expr = expr.split('->') >>> inputs_expr = qry_expr.split(',') >>> inputs_expr, res_expr (['ij', 'jk'], 'ki') -
Znajdź unikalne klucze (etykiety ) w indeksie dolnym wejściowym:
>>> keys = set([(key, size) for keys, input in zip(inputs_expr, inputs) for key, size in list(zip(keys, input.shape))]) {('i', 3), ('j', 4), ('k', 2)}Powinniśmy sprawdzać ograniczenia (jak również w wyjściowym indeksie dolnym)! Używanie
setjest złym pomysłem, ale będzie działać na potrzeby tego przykładu. -
Potrzebujemy listy zawierającej klucze (etykiety):
>>> to_key = [key for key, _ in keys] ['k', 'i', 'j'] -
Pobierz powiązane rozmiary (używane do inicjalizacji tablicy wyjściowej) i skonstruuj zakresy (używane do tworzenia naszej domeny iteracji):
>>> sizes = {key: size for key, size in keys} {'i': 3, 'j': 4, 'k': 2} >>> ranges = [range(size) for _, size in keys] [range(0, 2), range(0, 3), range(0, 4)] -
Oblicz iloczyn kartezjański
ranges>>> domain = product(*ranges)Strzeż się:
itertools.productzwraca iterator, który z czasem zostaje zużyty . -
Zainicjalizuj tensor wyjściowy jako:
>>> res = np.zeros([sizes[key] for key in res_expr]) -
Będziemy zapętlać
domain:>>> for indices in domain: ... passDla każdej iteracji,
indicesbędzie zawierać wartości na każdej osi. Dla naszego przykładu, że wartościi,j, ikjako krotka:(k, i, j). Jakbyśmy byli wewnątrz trzechforpętli. Dla każdego wejścia (AiB) musimy określić, który komponent pobrać. To jestA[i, j]iB[j, k], tak! Ale to nie wystarczy, ponieważ nie mamy zmiennychi,j, ik(dosłownie).Możemy zip
indiceszto_key, aby utworzyć mapowanie pomiędzy każdym kluczem (label ) i jego aktualną wartością:>>> vals= {k: v for v, k in zip(indices, to_key)}Aby uzyskać Współrzędne dla tablicy wyjściowej, używamy
valsi pętli nad klawiszami:[vals[key] for key in res_expr]. Jednak, aby użyć ich do indeksowania tablicy wyjściowej, musimy owinąć jątupleizip, aby oddzielić indeksy wzdłuż każdej osi:>>> res_ind = tuple(zip([vals[key] for key in res_expr]))To samo dla indeksów wejściowych (choć może być ich kilka):
>>> inputs_ind = [tuple(zip([vals[key] for key in expr])) for expr in inputs_expr] -
Użyjemy
itertools.reduceaby obliczyć iloczyn wszystkich wnoszących wkład składniki:>>> def reduce_mult(L): ... return reduce(lambda x, y: x*y, L) -
Ogólnie pętla nad domeną wygląda następująco:
>>> for indices in domain: ... vals = {k: v for v, k in zip(indices, to_key)} ... res_ind = tuple(zip([vals[key] for key in res_expr])) ... inputs_ind = [tuple(zip([vals[key] for key in expr])) ... for expr in inputs_expr] ... ... res[res_ind] += reduce_mult([M[i] for M, i in zip(inputs, inputs_ind)])
>>> res
array([[70., 44., 65.],
[30., 59., 68.]])
*Phew * , to całkiem blisko np.einsum('ij,jk->ki', A, B)!
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2021-02-03 07:53:12
Myślę, że najprostszy przykład jest w TensorFlow docs
Istnieją cztery kroki, aby przekształcić równanie w notację einsum. Weźmy to równanie jako przykład C[i,k] = sum_j A[i,j] * B[j,k]
- najpierw upuszczamy nazwy zmiennych. Otrzymujemy
ik = sum_j ij * jk - rezygnujemy z
sum_jterminu, ponieważ jest on niejawny. Otrzymujemyik = ij * jk - zamieniamy
*na,. Otrzymujemyik = ij, jk - wyjście jest na RHS i jest oddzielone znakiem
->. Otrzymujemyij, jk -> ik
Einsum interpreter po prostu uruchamia te 4 kroki w odwrotnej kolejności. Wszystkie wskaźniki brakujące w wyniku są sumowane.
Oto kilka przykładów z dokumentów
# Matrix multiplication
einsum('ij,jk->ik', m0, m1) # output[i,k] = sum_j m0[i,j] * m1[j, k]
# Dot product
einsum('i,i->', u, v) # output = sum_i u[i]*v[i]
# Outer product
einsum('i,j->ij', u, v) # output[i,j] = u[i]*v[j]
# Transpose
einsum('ij->ji', m) # output[j,i] = m[i,j]
# Trace
einsum('ii', m) # output[j,i] = trace(m) = sum_i m[i, i]
# Batch matrix multiplication
einsum('aij,ajk->aik', s, t) # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2020-07-08 05:03:16