Wyjaśnij, jak działa wyszukiwanie węzła startowego cyklu w liście połączonej z cyklem?

Pozwól, że spróbuję wyjaśnić algorytm wykrywania cyklu, który jest dostarczany w http://en.wikipedia.org/wiki/Cycle_detection#Tortoise_and_hare [[23]} własnymi słowami.

Odwołuję się do rysunku 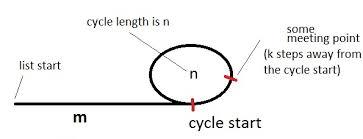W moim wyjaśnieniu.

Jak to działa

Niech Żółw i zając (nazwa wskaźników) wskazują na początek listy cyklem.

Przypuśćmy, że jeśli poruszamy żółwia 1 krok na raz, a zająca 2 kroki na raz, w końcu spotkają się w pewnym momencie. Pokażmy, że przede wszystkim ta hipoteza jest prawdziwa.

Rysunek ilustruje listę z cyklem. Cykl ma długość n i jesteśmy początkowo m krok od cyklu. Załóżmy również, że miejsce spotkania jest k krok od początku cyklu, a żółw i zając spotykają się po sumie i kroków.

Muszą być spełnione 2 następujące warunki:

1) i = m + p * n + k

2) 2i = m + q * n + k

Pierwszy mówi, że żółw porusza się i krokami i w tych krokach i najpierw dochodzi do cyklu. Następnie przechodzi przez cykl p razy dla pewnej liczby dodatniej p. W końcu przechodzi przez k więcej węzłów, aż spotyka hare ' a.

Podobnie jest z zającem. Porusza się 2i krokami i w tych 2i krokach najpierw dociera do cyklu. Następnie przechodzi przez cykl q razy dla pewnej liczby dodatniej q. W końcu przechodzi przez k więcej węzłów, aż spotyka żółwia.

Jak zając podróżuje z podwójną prędkością żółwia, a czas jest stały dla obu, gdy docierają do miejsca spotkania.

Więc używając prostej relacji prędkości, czasu i odległości,

2 ( m + p * n + k ) = m + q * n + k

=> 2m + 2pn + 2k = m + nq + k 

=>  m + k = ( q - 2p ) n

Wśród m, n, k, p, q dwa pierwsze są właściwościami danej listy. Jeśli możemy pokazać, że istnieje co najmniej jeden zbiór wartości dla k, q, p, który sprawia, że to równanie jest prawdziwe, pokazujemy, że hipoteza jest poprawna.

Jeden taki zestaw rozwiązań jest następujący:

p = 0

q = m

k = m n - m

Możemy sprawdzić, czy te wartości działają jak następuje:

m + k = ( q - 2p ) n  

=> m + mn - m = ( m - 2*0) n

=> mn = mn.

Dla tego zbioru i jest

i = m + p n + k

=> m + 0 * n + mn - m = mn.

Oczywiście powinieneś zobaczyć, że niekoniecznie jest to najmniejszy i możliwy. Innymi słowy, Żółw i zając mogły już spotkać się wcześniej wiele razy. Ponieważ jednak pokazujemy, że spotykają się w pewnym momencie przynajmniej raz, możemy powiedzieć, że hipoteza jest poprawna. Więc musieliby się spotkać, gdybyśmy przenieśli jeden z nich 1 krok, a drugi 2 kroki na raz.

Teraz możemy przejść do drugiej części algorytmu czyli jak znaleźć początek cyklu.

Początek Cyklu

Kiedy Żółw i zając się spotkają, odstawmy żółwia z powrotem na początek listy i zachowajmy zająca tam ,gdzie się spotkali (czyli krok k Od początku cyklu).

Hipoteza jest taka, że jeśli pozwolimy im poruszać się z tą samą prędkością( 1 krok dla obu), pierwszy raz spotkają się ponownie będzie początkiem cyklu.

Załóżmy najpierw jakaś wyrocznia mówi nam, czym jest M.

Wtedy, jeśli pozwolimy im przenieść m + k kroki, żółw musiałby dotrzeć do punktu, który spotkał się pierwotnie (kroki k Od początku cyklu-patrz na rysunku).

Poprzednio to pokazywaliśmy m + k = (q - 2p) n.

Ponieważ m + k kroki jest wielokrotnością długości cyklu n, hare, w średnim czasie, przejdzie przez cykl (q-2p) razy i wróci do tego samego punktu(K kroki od początku cyklu).

Teraz, zamiast pozwalając im poruszać się m + k kroki, jeśli pozwolimy im poruszać się tylko M kroki, żółw pojawi się na początku cyklu. Zając byłby k krok krótki od zakończenia (q-2P) rotacji. Ponieważ zaczął K kroki przed rozpoczęciem cyklu, zając musiałby przybyć na początku cyklu.

W rezultacie wyjaśnia to, że muszą się spotkać na początku cyklu po pewnej liczbie kroków po raz pierwszy (bardzo pierwszy raz, ponieważ żółw przybył właśnie na cykl po krokach m i nigdy nie było widać zająca, który był już w cyklu).

Teraz wiemy, że liczba kroków, które musimy przesunąć, aż się spotkają, okazuje się odległością od początku listy do początku cyklu, m. oczywiście algorytm nie musi wiedzieć, co to jest m. Po prostu poruszy zarówno żółwia, jak i zająca krok po kroku, aż się spotkają. Punktem spotkania musi być początek cyklu, a liczba kroków musi być odległością (m) do początku cyklu. Zakładając, że znamy długość listy, możemy również obliczyć długość cyklu odejmowania m od długości listy.

Zobacz to zdjęcie:

Odległość pokonana przez slowPointer przed spotkaniem = x + y

Odległość pokonana przez fastPointer przed spotkaniem = (x + y + z) + y = x + 2y + z

Ponieważ fastPointer podróżuje z podwójną prędkością slowpointera, a Czas jest stały dla obu, gdy dotrze do miejsca spotkania.

Więc używając prosta relacja prędkości, czasu i odległości 2 (x+y)= x + 2y + z => x+2Y+z = 2x+2Y = > x = z

Stąd przesuwając slowPointer na początek połączonej listy i sprawiając, że zarówno slowPointer, jak i fastPointer poruszają się po jednym węźle na raz, oba mają taką samą odległość do pokrycia.

Osiągną punkt, w którym pętla zaczyna się na liście połączonej.

_{prosta odpowiedź Starego mnicha wyjaśnia znalezienie cyklu, gdy szybki biegacz ukończy tylko jeden pełny cykl. W tej odpowiedzi wyjaśniam przypadek, gdy fast runner wielokrotnie uruchamiał pętlę, zanim powolny biegacz wejdzie w pętlę.}

Używanie tego samego obrazu:

Załóżmy, że szybki biegacz uruchomił pętlę M razy, zanim powoli i szybko się spotkają. Oznacza to, że:

• dystans przebiegający powoli: x + y
• dystans przebiegający szybko: x + m(y + z) + y tj. extra y gdzie spotykają się

Ponieważ szybkie biegi z dwukrotnie większą prędkością niż powolne i że biegły przez ten sam czas, oznacza to, że jeśli podwoimy dystans przejechany przez powolne, otrzymamy dystans przejechany przez szybkie. Zatem

• 2(x + y) = X + m (y + z) + y

Rozwiązywanie dla X daje,

x = (m-1) (y + z) + Z

In real scenariusz oznaczałby, x = (m-1) pełne biegi pętli + dodatkowy dystans z .

Stąd, jeśli umieścimy jeden wskaźnik na początku listy i zostawimy drugi na miejscu spotkania, wtedy przesunięcie go o tę samą prędkość spowoduje, że wskaźnik in loop zakończy M - 1 Biegi pętli, a następnie spotka drugi wskaźnik tuż na początku pętli.

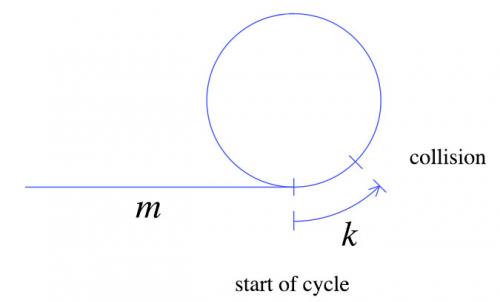
W momencie pierwszej kolizji żółw ruszył m + k kroki jak pokazano powyżej. Zając porusza się dwa razy szybciej niż żółw, czyli zając porusza się 2(m + k) Kroki. Z tych prostych faktów możemy wyprowadzić następujący wykres.

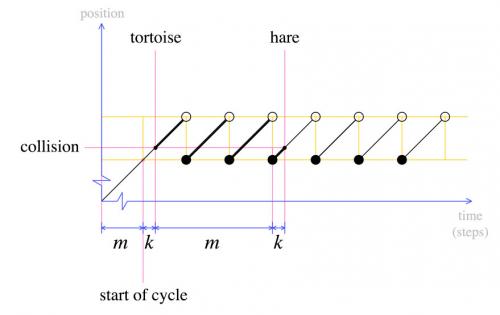
W tym momencie przenosimy żółwia z powrotem na początek i deklarujemy, że zarówno zając, jak i żółw muszą poruszać się krok po kroku. Z definicji, po na Kroki, żółw będzie na początku cyklu. Gdzie będzie hare?

Zając będzie również na początku cyklu. Widać to wyraźnie z drugiego wykresu: kiedy żółw został przeniesiony z powrotem na początek, zając był k Kroki do ostatniego cyklu. Po na Kroki, zając ukończy kolejny cykl i zderzy się z żółwiem.

Dobrze więc załóżmy, że zając i żółw spotykają się w punkcie, który jest K kroków od początku cyklu, liczba kroków przed rozpoczęciem cyklu jest mu, a długość cyklu jest L.

Więc teraz w miejscu spotkania - >

Odległość pokonana przez żółwia = mu + A*L + K-równanie 1

(kroki podjęte w celu osiągnięcia początku cyklu + kroki podjęte w celu pokrycia iteracji " a " cyklu + kroki k Od początku cyklu) (gdzie A jest jakimś pozytywnym stała)

Odległość pokonana przez zająca = mu + b*L + K-równanie 2

(kroki podjęte w celu osiągnięcia początku cyklu + kroki podjęte w celu pokrycia iteracji " b " cyklu + kroki k Od początku cyklu) (gdzie b jest pewną stałą dodatnią i b> = A)

Tak więc dodatkowa odległość pokonana przez zająca wynosi = równanie 2-równanie 1 = (b-a) * L

Należy pamiętać, że odległość ta jest również równa odległości żółwia od punktu wyjścia, ponieważ zając porusza się 2 razy szybciej niż żółw. Można to przyrównać do "mu + k", która jest również odległością miejsca spotkania od początku, jeśli nie uwzględnimy wielokrotnych przejazdów cyklu.

Tak więc, mu + k = (b-a) * L

Tak więc kroki mu od tego punktu prowadziłyby z powrotem do początku cyklu (ponieważ kroki k Od początku cyklu zostały już podjęte, aby dotrzeć do miejsca spotkania). Może to nastąpić w tym samym cyklu lub w każdym z kolejnych cykli. Tak więc teraz, jeśli ruszymy żółw do początku powiązanej listy, podejmie kroki mu, aby osiągnąć punkt początkowy cyklu i zając podejmie kroki mu, aby również dotrzeć do początku cyklu, a tym samym obaj spotkają się w punkcie początkowym cyklu.

P. S. szczerze mówiąc, miałem w głowie to samo pytanie, co oryginalny plakat i przeczytałem pierwszą odpowiedź, wyczyścili kilka rzeczy, ale nie mogłem wyraźnie dotrzeć do ostatecznego wyniku, więc starałem się zrobić to po swojemu i znalazłem to łatwiejsze zrozumieć.

To bardzo, bardzo proste. Można myśleć w kategoriach względnej prędkości. Jeśli królik porusza się dwoma węzłami, a żółw porusza się jednym węzłem, w stosunku do żółwia królik porusza się jednym węzłem (Załóżmy, że żółw w spoczynku). Tak więc, jeśli przeniesiemy jeden węzeł na okrągłej liście połączonej, na pewno spotkamy się w tym punkcie ponownie.

Po znalezieniu punktu połączonego wewnątrz okrągłej listy połączonej, problem sprowadza się do znalezienia punktu przecięcia dwóch połączonych list.

Podejście:

Istnieją dwa wskaźniki:

• powolny wskaźnik, który porusza się po jednym węźle na raz.
• szybki wskaźnik, który przesuwa dwa węzły na raz.

Jeśli dwa wskaźniki spełniają się, dowodzi to, że istnieje pętla. Gdy się spotkają, jeden z węzłów wskaże głowę, a następnie oba będą postępować po jednym węźle na raz. Spotkają się na początku pętli.

Uzasadnienie: Kiedy dwie osoby chodzą po okrągłym torze, jeden z nich z prędkością dwa razy większą od drugiego, gdzie się spotykają? Dokładnie tam, gdzie zaczęli.

Przypuśćmy, że szybki biegacz ma przewagę k kroków w okrążeniu n. gdzie się spotkają? Dokładnie na n-k krokach. Gdy wolny biegacz zakryje (n-k) kroki, szybki biegacz zakryje k+2(n-k) kroki. (ie, k+2n-2k kroki ie 2n-k kroki). tj. (n-k) kroki (ścieżka jest okrągła i nie przejmujemy się liczbą rund, po których się spotykają; jesteśmy po prostu zainteresowany pozycją, w której się spotykają).

Jak szybko biegacz dostał przewagę k kroków w pierwszej kolejności? Ponieważ powolnemu biegaczowi zajęło to wiele kroków, aby dotrzeć do początku pętli. Tak więc początek pętli to kroki k od węzła głównego.

Uwaga: węzeł, w którym spełnione są oba wskaźniki jest k krok od początku pętli (wewnątrz pętli), a węzeł główny jest również k krok od początku pętli. Więc kiedy mamy wskazówkę w równym tempie 1 kroku od bota te węzły spotkają się na początku pętli.

Uważam, że jest to proste. Proszę dać mi znać, jeśli jakaś część jest niejednoznaczna.

Zmniejsz problem do problemu pętli, a następnie wróć do początkowego problemu

Poniższe wyjaśnienie wydaje mi się bardziej intuicyjne.

1. Weź dwa wskazówki (1 = Żółw i 2 = zając), które zaczynają się od głowy (O), 1 ma długość kroku 1, 2 ma długość kroku 2. Pomyśl o chwili, kiedy 1 dociera do węzła początkowego tego cyklu (A ).

   Chcemy odpowiedzieć na następujące pytanie "gdzie jest 2, Gdy 1 jest w A?".

   Zatem OA = a jest liczbą naturalną (a >= 0). Ale można go zapisać w następujący sposób: a = k*n + b, Gdzie a, k, n, b are natural numbers:

   • n = długość cyklu
   • k >= 0 = stała
   • 0 <= b <= n-1

   Oznacza to, że b = a % n.

   Np.: jeśli a = 20 i n = 8 => k = 2 i b = 4 ponieważ 20 = 2*8 + 4.

   Odległość pokonana przez 1 na d = OA = a = k*n + b. Ale w tym samym czasie, 2 okładki D = 2*d = d + d = OA + d = OA + k*n + b. Oznacza to, że gdy 2 jest w to musi obejmować k*n + b. Jak widać, k jest liczbą okrążeń, ale po tych okrążeniach, 2 będzie B daleko od A. więc znaleźliśmy, gdzie 2 jest kiedy 1 jest w A. nazwijmy to punktem B, gdzie AB = b.

   

2. Teraz zredukujemy problem do koła. Pytanie brzmi " gdzie jest spotkanie punkt?". Gdzie jest to C ?

   

   Na każdym kroku, 2 zmniejsza odległość od 1 Z 1 (powiedzmy licznik), ponieważ 1 jest coraz dalej od 2 Z 1, ale jednocześnie 2 zbliża się do 1 by 2.

   Więc skrzyżowanie będzie wtedy, gdy odległość między 1 oraz 2 będzie zero. Oznacza to, że 2 zmniejsza n - b odległość. W tym celu, 1 uczyni n - b kroki, podczas gdy 2 zrobi 2*(n - b) kroki.

   Więc punkt przecięcia będzie n - b daleko od A (zgodnie z ruchem wskazówek zegara), ponieważ jest to odległość pokonana przez 1 dopóki się nie spełni 2. = > odległość między C a A wynosi CA = b, ponieważ AC = AB + BC = n - b i CA = n - AC. Nie myśl, że AC = CA, ponieważ AC odległość nie jest trywialną odległością matematyczną, jest liczba kroków pomiędzy A a C (gdzie A jest punktem początkowym, a C jest punktem końcowym).

3. Wróćmy do początkowego schematu.

   Wiemy, że a = k*n + b i CA = b.

   Możemy wziąć 2 nowe wskazówki 1' oraz 1", gdzie 1' zaczyna się od głowy (O ) I 1" rozpoczyna się od punktu przecięcia (C ).

   While 1' goes from O do A, 1" przechodzi od C do A i kończy k okrążenia. Punkt przecięcia to A .

   

   

Jeśli wskaźniki spotkały się w punkcie P, Jak pokazano na rysunku, odległość z + Y to punkt P, A X + Y to również punkt P, co oznacza Z=X. dlatego utrzymanie ruchu jednego wskaźnika od P i przesunięcie drugiego od początku(S) do ich spełnienia, co oznacza przesunięcie równej odległości(Z lub X) do tego samego punktu M(odległość z od P I X od S) będzie początkiem pętli. Proste!

W rzeczywistości łatwo jest udowodnić, że oba spotkają się w punkcie wyjścia, jeśli weźmiemy pod uwagę matematykę za punktem spotkania.
Po pierwsze niech M oznacza punkt początkowy cyklu w połączonej liście, a n oznacza długość cyklu . Wtedy na spotkanie zająca i żółwia mamy:

( 2*t - m )%n = (t - m) %n, where t = time (at t = 0 , both are at the start)

Mówiąc to bardziej matematycznie:

(2*t - m - (t - m) ) = 0 modulo n , which implies , t = 0 modulo n 

Więc spotkają się w czasie t , który powinien być wielokrotnością długości cyklu . Oznacza to, że spotykają się w miejscu, które jest (t-m) modulo n = (0-m) modulo n = (-m) modulo n .

Więc teraz wracając do pytania, jeśli przesuniesz jeden wskaźnik od początku połączonej listy , a drugi od punktu przecięcia , po krokach m Będziemy mieli zająca (który porusza się wewnątrz cyklu) do punktu, który jest ((-m) + m) modulo n = 0 modulo n, który jest niczym innym, jak punktem wyjścia listy. cycle.So widzimy, że po krokach m dochodzi do początku cyklu i żółw spotka go tam, gdy przemierzy M kroki z początek połączonej listy.

Na marginesie ,możemy również obliczyć czas ich przecięcia w ten sposób : warunek t = 0 modulo n mówi nam, że spotkają się w czasie, który jest wielokrotnością długości cyklu, a także tpowinien być większy niż m, Jak spotkałyby się w cyklu . Tak więc czas będzie równy pierwszej wielokrotności n, która jest większa niż m .

Przy wszystkich powyższych analizach, jeśli jesteś osobą ucząc się przez przykład, próbowałem napisać krótką analizę i przykład, który pomoże wyjaśnić matematykę, którą wszyscy próbowali wyjaśnić. Zaczynamy!

Analiza:

Jeśli mamy dwa wskaźniki, jeden szybciej niż drugi, i przesuwamy je razem, w końcu spotkają się ponownie, aby wskazać cykl lub null, aby wskazać brak cyklu.

Aby znaleźć punkt początkowy cyklu, niech ...

1. m be odległość od głowy do początku cyklu;
2. d być liczbą węzłów w cyklu;
3. p1 być prędkością wolniejszego wskaźnika;

4. p2 Być prędkością szybszego wskaźnika, np. 2 oznacza kroki przez dwa węzły na raz.

   Obserwuj następujące iteracje:

 m = 0, d = 10:
 p1 = 1:  0  1  2  3  4  5  6  7  8  9 10 // 0 would the start of the cycle
 p2 = 2:  0  2  4  6  8 10 12 14 16 18 20

 m = 1, d = 10:
 p1 = 1: -1  0  1  2  3  4  5  6  7  8  9
 p2 = 2: -1  1  3  5  7  9 11 13 15 17 19

 m = 2, d = 10:
 p1 = 1: -2 -1  0  1  2  3  4  5  6  7  8
 p2 = 2: -2  0  2  4  6  8 10 12 14 16 18

Z powyższych przykładowych danych możemy łatwo odkryć, że ilekroć szybsze i wolniejsze wskaźniki spotykają się, są one oddalone o krok od początku cyklu. Aby to rozwiązać, umieść szybszy wskaźnik z powrotem na głowie i ustaw jego prędkość na prędkość wolniejszego wskaźnika. Gdy spotykają się ponownie, węzeł jest początkiem cyklu.

Powiedzmy,

N[0] is the node of start of the loop, 
m is the number of steps from beginning to N[0].

Mamy 2 wskaźniki A i B, A działa z prędkością 1x, B z prędkością 2x, oba zaczynają się na początku.

Gdy A osiągnie N [0], B powinien być już w N [m]. (Uwaga: A używa kroków m, aby osiągnąć N[0] , A B powinno być krokami m dalej)

Następnie, a biegnie k więcej kroków, aby zderzyć się z B, tj. A jest na N [k], B jest na N [m+2k] (UWAGA: B powinien działać dla 2k kroków począwszy od N [m])

Zderzenie B odpowiednio na N [k] I N[m+2K], oznacza k = m+2K, a więc k = -m

Tak więc, aby powrócić do N[0] z N [k], potrzebujemy m więcej kroków.

Mówiąc po prostu, musimy po prostu uruchomić m więcej kroków po znalezieniu węzła kolizji. Możemy mieć wskaźnik do uruchomienia od początku i wskaźnik do uruchomienia od węzła kolizji, spotkają się one przy N [0] po krokach m.

Zatem pseudo kod jest następujący:

1) A increase 1 step per loop
2) B increase 2 steps per loop
3) if A & B are the same node, cycle found, then go to 5
4) repeat from 1
5) A reset to head
6) A increase 1 step per loop
7) B increase 1 step per loop
8) if A & B are the same node, start of the cycle found
9) repeat from 6

Nie sądzę, że to prawda, że kiedy się spotykają, to punkt wyjścia. Ale tak, jeśli drugi wskaźnik(F) był wcześniej w miejscu spotkania , niż ten wskaźnik będzie na końcu pętli zamiast na początku pętli, a wskaźnik (Y), który rozpoczął się od początku listy, skończy się na początku pętli. dla NP:

1->2->3->4->5->6->7->8->9->10->11->12->13->14->15->16->17->18->19->20->21->22->23->24->8

Meet at :16

Start at :8

public Node meetNodeInLoop(){

    Node fast=head;
    Node slow=head;

    fast=fast.next.next;
    slow=slow.next;

    while(fast!=slow){

        fast=fast.next;
        fast=fast.next;

        if(fast==slow) break; 

        slow=slow.next;
    }

    return fast;

}

public Node startOfLoop(Node meet){

    Node slow=head;
    Node fast=meet;

    while(slow!=fast){
        fast=fast.next;
        if(slow==fast.next) break;
        slow=slow.next;
    }

    return slow;
}

Proste wyjaśnienie wykorzystujące ideę prędkości względnej nauczanej w liceum-wykłady z fizyki 101 / kinematyki.

1. Załóżmy, że odległość od początku połączonej listy do początku okręgu wynosi x. Początek okręgu nazywamy punktem X (w caps-patrz rysunek powyżej). Załóżmy również, że całkowita wielkość okręgu wynosi N.

2. Prędkość zająca = 2 * Prędkość żółwia. Czyli 1 hops/sec i 2 hops/sec

3. Gdy żółw dotrze do początku okręgu X, zając musi być dalej x przeskakując w punkcie Y na rysunku. (Bo zając przebył dwa razy większą odległość niż żółw).

4. Tak więc długość pozostałego łuku zgodnie z ruchem wskazówek zegara od X do Y wynosiłaby N-x. T jego również jest względną odległością do pokonania między zającem a żółwiem, aby mogli się spotkać[54]}. Powiedzmy, że ta odległość względna będzie pokryte w czasie t_m, tj. czas na spotkanie. Prędkość względna wynosi (2 hops/sec - 1 hops/sec) tj. 1 hops/sec. W ten sposób, używając odległości względnej = prędkości względnej X czasu, otrzymujemy, t = N-x sec. więc to zajmie N-x, aby dotrzeć do miejsca spotkania zarówno żółwia i zająca.

5. Teraz w czasie N-x SEK i z prędkością 1 hops/sec, żółw, który był wcześniej w punkcie X, pokryje n-x chmielu, aby dotrzeć do miejsca spotkania M. Oznacza to, że miejsce spotkania M znajduje się w N-x w kierunku przeciwnym do ruchu wskazówek zegara od X = (co dodatkowo implikuje) => że istnieje x odległość pozostała od punktu M do X zgodnie z ruchem wskazówek zegara.

6. Ale x jest również odległością do punktu X Od początku połączonej listy.

7. Nie obchodzi nas, jaka liczba chmielu x odpowiada. Jeśli umieścimy jednego żółwia na początku LinkedList i jednego żółwia na miejscu spotkania M i pozwolimy im skakać/chodzić, to spotkają się w punkcie X, który jest punktem (lub węzłem), który potrzeba.

Praca z diagramem by pomogła. Staram się wyjaśnić problem bez równań.

Jeśli pozwolimy zającowi i żółwiowi biegać w kole, a zając biega dwa razy ŻÓŁW, to na końcu jednego okrążenia żółw zając będzie w połowie. Na koniec dwóch okrążeń z Hare żółw zrobiłby 1 okrążenie i obaj spotykają się. Dotyczy to wszystkich prędkości, jak jeśli hare biegnie trzy razy, hare 1 okrążenie jest równe 1/3 żółwia, więc na koniec 3 okrążeń dla żółwia zajęczego obejmowałby 1 okrążenie i spotykają się.
1. Teraz jeśli zaczniemy je m kroki przed pętli, to oznacza, że szybciej zając zaczyna się przed pętli. Więc jeśli żółw dotrze do początku pętli, zając będzie m kroków przed pętlą, a gdy się spotkają, będzie M kroków przed rozpoczęciem pętli.

W większości rozwiązań tego problemu występuje błąd. Co jeśli ostatni węzeł był połączony z pierwszym i była to po prostu pętla? Co jeśli powolny i szybki spotkają się na czele pętli za pierwszym razem? Nie znajdziesz poprawnej odpowiedzi w tym rozwiązaniu. Istnieje poprawna odpowiedź, jak uniknąć tej sytuacji, ale biorąc pod uwagę szczęśliwą ścieżkę, z liczbą węzłów k przed pętlą, oto proste wyjaśnienie: (jeśli chcesz dowiedzieć się więcej o rzeczywistym, uogólnionym rozwiązaniu, ping me)

- przed pętlą są kroki K. Nie wiemy, co to jest k i nie musimy się tego dowiedzieć. Możemy pracować abstrakcyjnie za pomocą tylko k.

--po krokach k

----- T jest na początku cyklu

----- H jest k kroki w cyklu (poszedł 2k razem, a tym samym k W pętli)

* * są teraz loopsize-K apart

(zauważ, że k = = K = = mod (loopsize, k) --np. jeśli węzeł ma 2 kroki w cyklu 5 węzłów, to również 7, 12 lub 392 kroki, więc jak duży jest ten cykl w. r. T k nie bierze pod uwagę.

Ponieważ doganiają się nawzajem w tempie 1 kroku na jednostkę czasu, ponieważ jeden porusza się dwa razy szybciej niż drugi, spotkają się w loopsize-K.

Oznacza to, że zajmie węzły k, aby dotrzeć do początku cyklu, a zatem odległość od głowy do cyclestart i kolizji do cyclestart są takie same.

Więc teraz po pierwszej kolizji przesuń T z powrotem do głowy. T I H spotkają się na cyclestart, jeśli poruszasz się z szybkością 1 każdy. (w krokach k dla obu)

Oznacza to, że algorytm jest:

• z ruchu głowy T = T. następny i H. następny.następnie, aż zderzą się (T = = H) (istnieje cykl)

/ / zadbaj o przypadek, gdy K=0 lub T I H spotkają się na czele pętli przez obliczanie długości pętli

-- policz długość cyklu przesuwając T lub H wokół niego licznikiem

-- Przenieś wskaźnik T2 na początek listy

-- przesuń wskaźnik długości kroków cyklu

-- move another wskaźnik H2 do głowy

--przesuń T2 i H2 w tandemie, aż spotkają się na początku cyklu

To jest to!

Wiem, że istnieje już akceptowana odpowiedź na ten problem, ale nadal postaram się odpowiedzieć płynnie. Zakładać:

The length of the Path is 'X+B' where 'B' is the length of the looped path and X of the non looped path. 
    Speed of tortoise : v
    Speed of hare     : 2*v 
    Point where both meet is at a distance 'x + b - k' from the starting point.

Uwagi:

If, Distance traveled by the tortoise = v*t = x + (b-k) (say)

Następnie, odległość przebyta przez zająca = 2 * v * t = x + (b-k) + b (ponieważ zając już raz przemierzył zapętloną część)

Teraz są czasy spotkań to samo.

= > x + 2 * b-k = 2 *(x + b - k)

= > x = k

Oznacza to oczywiście, że długość ścieżki, która nie jest zapętlona, jest taka sama jak odległość punktu początkowego pętli od punktu, w którym spotykają się obie.