Czy lookaround wpływa na to, które języki mogą być dopasowane przez wyrażenia regularne?

Odpowiedź na pytanie, które zadajesz, czyli czy większa Klasa języków niż języki regularne może być rozpoznana za pomocą wyrażeń regularnych rozszerzonych przez lookaround, brzmi nie.

Dowód jest stosunkowo prosty, ale algorytm tłumaczenia wyrażenia regularnego zawierającego lookarounds na jedno Bez jest niechlujny.

Po pierwsze: zauważ, że zawsze możesz zanegować Wyrażenie regularne (ponad skończonym alfabetem). Biorąc pod uwagę skończony automat stanu, który rozpoznaje język generowane przez wyrażenie, można po prostu wymienić wszystkie akceptujące Stany NA nieakceptujące Stany, aby uzyskać FSA, który rozpoznaje dokładnie negację tego języka, dla którego istnieje rodzina równoważnych wyrażeń regularnych.

Po drugie: ponieważ języki regularne (a więc wyrażenia regularne) są zamknięte pod negacją, są również zamknięte pod przecięciem, ponieważ przecięcie B = neg(neg (a) union neg (B)) przez prawa De Morgana. Innymi słowy podane dwa wyrażenia regularne, możesz znaleźć inne wyrażenie regularne, które pasuje do obu.

Pozwala to na symulację wyrażeń lookaround. Na przykład u (?=v) w dopasowuje tylko wyrażenia, które będą pasowały do uv i uw.

Dla ujemnego spojrzenia potrzebujesz wyrażenia regularnego równoważnego zbioru teoretycznego A\B, który jest po prostu przecięciem (neg B) lub równoważnym neg (neg (a) Związek B). Tak więc dla dowolnych wyrażeń regularnych r I s można znaleźć wyrażenie regularne r-s, które pasuje do tych wyrażeń, które pasują do r które nie pasują do s. w negatywnym znaczeniu: u (?!v) W pasuje Tylko do tych wyrażeń, które pasują do uw-uv.

Są dwa powody, dla których lookaround jest przydatny.

Po pierwsze, ponieważ negacja wyrażenia regularnego może skutkować czymś znacznie mniej uporządkowanym. Na przykład q(?!u)=q($|[^u]).

Po Drugie, wyrażenia regularne robią więcej niż pasują do wyrażeń, zużywają również znaki z łańcucha znaków-a przynajmniej tak lubimy o nich myśleć. Na przykład w Pythonie zależy mi na .start () i .end (), stąd oczywiście:

>>> re.search('q($|[^u])', 'Iraq!').end()
5
>>> re.search('q(?!u)', 'Iraq!').end()
4

Po Trzecie, i myślę, że jest to dość ważny powód, negacja wyrażeń regularnych nie podnosi ładnie nad konkatenacją. neg (a) neg (b) nie jest tym samym co neg(ab), co oznacza, że nie możesz przetłumaczyć lookaround z kontekstu, w którym go znajdujesz - musisz przetworzyć cały łańcuch. Myślę, że to sprawia, że praca z ludźmi jest nieprzyjemna i łamie ludzkie intuicje dotyczące wyrażeń regularnych.

I hope I odpowiedziałem na pytanie teoretyczne (jego późno w nocy, więc wybacz mi, jeśli jestem niejasny). Zgadzam się z komentatorem, który powiedział, że ma to praktyczne zastosowanie. Ten sam problem napotkałem podczas próby zeskrobania bardzo skomplikowanych stron internetowych.

EDIT

Przepraszam, że nie jestem jaśniejszy: nie wierzę, że można dać dowód regularności wyrażeń regularnych + szukać przez indukcję strukturalną, mój u (?!v) w przykładzie miało być właśnie to, an przykład, i to prosty. Powodem, dla którego indukcja strukturalna nie będzie działać, jest to, że lookarounds zachowuje się w sposób nie-kompozytowy - punkt, który starałem się zrobić o negacjach powyżej. Podejrzewam, że jakikolwiek bezpośredni dowód formalny będzie zawierał wiele brudnych szczegółów. Próbowałem wymyślić łatwy sposób, aby to pokazać, ale nie mogę wymyślić jednego z czubków mojej głowy.

Aby zilustrować używając pierwszego przykładu ^([^a]|(?=..b))*$ jest to odpowiednik 7 stanu DFSA ze wszystkimi Stanami przyjmujący:

A - (a) -> B - (a) -> C --- (a) --------> D 
Λ          |           \                  |
|          (not a)       \               (b)
|          |              \               | 
|          v                \             v
(b)        E - (a) -> F      \-(not(a)--> G  
|            <- (b) - /                   |
|          |                              |
|         (not a)                         |
|          |                              |
|          v                              |
\--------- H <-------------------(b)-----/

Wyrażenie regularne dla samego stanu a wygląda następująco:

^(a([^a](ab)*[^a]|a(ab|[^a])*b)b)*$

Innymi słowy, każde wyrażenie regularne, które uzyskasz poprzez wyeliminowanie lookarounds, będzie ogólnie znacznie dłuższe i bardziej messier.

Odpowiadając na komentarz Josha - tak myślę, że najbardziej bezpośrednim sposobem udowodnienia równoważności jest FSA. Co sprawia, że ten messier jest to, że zwykły sposób konstruowania FSA jest za pomocą niedeterministycznej maszyny - jej znacznie łatwiej wyrazić u / v jako po prostu maszyna zbudowana z maszyn dla u I v z przejściem epsilon do dwóch z nich. Oczywiście jest to równoznaczne z maszyną deterministyczną, ale z ryzykiem wykładniczego wysadzenia Stanów. Natomiast negacja jest o wiele łatwiejsza do zrobienia za pomocą deterministycznej maszyny.

Dowód ogólny będzie polegał na pobraniu iloczynu kartezjańskiego dwóch maszyn i wybraniu tych stanów, które chcesz zachować w każdym punkcie, który chcesz wstawić. Powyższy przykład ilustruje co mam na myśli w pewnym stopniu.

DALSZA EDYCJA: Znalazłem post na blogu , który opisuje algorytm generowania DFA z wyrażenia regularnego rozszerzonego o lookarounds. Jego schludne, ponieważ autor rozszerza ideę NFA-e z "tagged epsilon transitions" w oczywisty sposób, a następnie wyjaśnia, jak przekształcić taki automat w DFA.

Myślałem, że coś takiego będzie sposobem na to, ale Cieszę się, że ktoś to napisał. Nie mogłem wymyślić czegoś tak schludnego.

Zgadzam się z innymi postami, że lookaround jest regularny (co oznacza, że nie dodaje żadnych podstawowych możliwości do wyrażeń regularnych), ale mam na to argument, który jest IMO prostszy niż inne, które widziałem.

Pokażę, że lookaround jest regularny, dostarczając konstrukcję DFA. Język jest regularny wtedy i tylko wtedy, gdy ma Dfa, który go rozpoznaje. Zauważ, że Perl nie używa DFAs wewnętrznie (szczegóły w tym artykule: http://swtch.com / ~rsc/regexp/regexp1.html ), ale dla celów dowodu konstruujemy DFA.

Tradycyjnym sposobem konstruowania DFA dla wyrażenia regularnego jest najpierw zbudowanie NFA za pomocą algorytmu Thompsona. Biorąc pod uwagę dwa fragmenty wyrażeń regularnych r1 i r2, algorytm Thompsona zapewnia konstrukcje dla konkatenacji (r1r2), alternacji (r1|r2) i powtórzeń (r1*) wyrażeń regularnych. Pozwala to na zbudowanie NFA bit po bitu, który rozpoznaje oryginalne Wyrażenie regularne. Więcej szczegółów można znaleźć w artykule powyżej.

Aby pokazać, że pozytywne i negatywne spojrzenia są regularne, przedstawię konstrukcję do konkatenacji wyrażenia regularnego u z pozytywnym lub negatywnym spojrzeniem: (?=v) lub (?!v). Tylko konkatenacja wymaga specjalnego traktowania; zwykłe konstrukcje naprzemienne i powtarzalne działają dobrze.

Konstrukcja jest dla obu u (?= v) i u(?!v) jest:

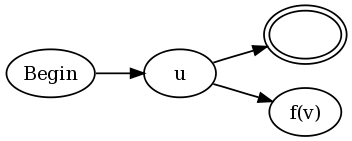
Innymi słowy, połącz każdy końcowy stan istniejącego NFA dla udo zarówno accept state , jak i do NFA dla v, ale zmodyfikowane w następujący sposób. Funkcja f(v) jest zdefiniowana jako:

• niech aa(v) będzie funkcją NA NFA v, która zmienia każdy stan accept w "stan anty-accept". Stan anty-accept jest zdefiniowany jako stan, który powoduje niepowodzenie dopasowania, jeśli Dowolna ścieżka przez NFA kończy się w tym stanie dla danego ciągu s, nawet jeśli inna ścieżka przez v dla s kończy się stanem accept.
• niech loop(v) będzie funkcją NA NFA v dodającą samo-przejście na dowolny stan accept. Innymi słowy, gdy ścieżka prowadzi do stanu accept, ścieżka ta może pozostać w stanie accept na zawsze, bez względu na to, jakie dane wejściowe nastąpią.
• dla negatywnego spojrzenia, f(v) = aa(loop(v)).
• dla pozytywnego spojrzenia, f(v) = aa(neg(v)).

Aby podać intuicyjny przykład, dlaczego to działa, użyję regex (b|a(?:.b))+, który jest nieco uproszczony wersja regex, którą zaproponowałem w komentarzach dowodu Franciszka. Jeśli użyjemy mojej konstrukcji wraz z tradycyjnymi konstrukcjami Thompsona, skończymy na: {]}

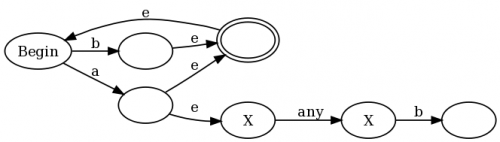
eS są przejściami epsilon (przejścia, które można wykonać bez zużywania jakichkolwiek danych wejściowych), a Stany anty-accept są oznaczone symbolem X. W lewej połowie wykresu widać reprezentację (a|b)+: any a lub b stawia wykres w stanie accept, ale pozwala również na przejście z powrotem do stanu początkowego, żebyśmy mogli to zrobić ponownie. Ale zauważ, że za każdym razem, gdy dopasujemy a, również wchodzimy w prawą połowę wykresu, gdzie jesteśmy w Stanach anty-accept, dopóki nie dopasujemy "any", po którym następuje b.

• = 1 Stany NFA to stan accept, i

• 0 Stany NFA są stanami anty-akceptującymi.

Algorytm ten da nam DFA, które rozpoznaje Wyrażenie regularne za pomocą lookahead. Ergo, lookahead jest regularny. Zauważ, że lookbehind wymaga osobnego dowodu.

Mam wrażenie, że zadaje się tu dwa różne pytania:

• są silnikami Regex, które encorporatują "lookaround" więcej potężne niż silniki Regex, które nie?
• Czy " lookaround" umożliwia Silnik Regex z możliwością parsowania języków, które są bardziej złożone niż te generowane przez Chomsky Typ 3 - gramatyka regularna ?

Odpowiedź na pierwsze pytanie w sensie praktycznym brzmi tak. Lookaround da Silnik Regex, który zastosowania cecha ta jest zasadniczo większa niż ta, która nie ma. dzieje się tak dlatego, że zapewnia bogatszy zestaw "kotwic" dla procesu dopasowania. Lookaround pozwala zdefiniować całe wyrażenie regularne jako możliwy punkt kontrolny (twierdzenie o zerowej szerokości). Możesz Pobierz całkiem dobry przegląd mocy tej funkcji tutaj .

Lookaround, choć mocny, nie podnosi silnika Regex poza teoretyczne ograniczenia nałożone na nią przez gramatykę typu 3. Na przykład nigdy nie będziesz w stanie niezawodnie analizowanie języka w oparciu o gramatykę Bezkontekstową typu 2 przy użyciu silnika Regex wyposażony w lookaround. Silniki Regex są ograniczone do mocy skończonej automatyzacji stanu a to zasadniczo ogranicza ekspresywność dowolnego języka, który mogą analizować do poziomu gramatyki typu 3. Nieważne. jak wiele "sztuczek" są dodawane do silnika Regex, języki generowane przez context free Grammar zawsze pozostanie poza jego możliwościami. Gramatyka Parsing Context Free-Type 2 wymaga automatyzacji pushdown, aby "zapamiętać", gdzie jest w rekurencyjna konstrukcja języka. Wszystko, co wymaga rekurencyjnej oceny reguł gramatycznych, nie może być analizowane za pomocą Silniki Regex.

Podsumowując: Lookaround zapewnia pewne praktyczne korzyści silnikom Regex, ale nie "zmienia gry" na poziom teoretyczny.

EDIT

Czy jest jakaś gramatyka ze złożonością gdzieś pomiędzy typem 3 (regularnym) a typem 2 (Bez Kontekstu)?

Myślę, że odpowiedź brzmi nie. Powodem jest to, że nie ma teoretycznego limitu umieszczony na rozmiarze NFA / DFA potrzebnym do opisania języka regularnego. Może stać się arbitralnie duża i dlatego niepraktyczne w użyciu(lub określeniu). To jest, gdzie Uniki takie jak "lookaround" są przydatne. Oni podaj mechanizm krótkiej ręki, aby określić, co w przeciwnym razie doprowadziłoby do bardzo dużego / złożonego NFA/DFA specyfikacje. Nie zwiększają ekspresji Języki regularne, po prostu sprawiają, że sprecyzowanie ich jest bardziej praktyczne. Po otrzymaniu tego punktu, staje się jasne, że istnieje wiele "funkcji", które można dodać do silników Regex, aby uczynić je bardziej przydatne w sensie praktycznym - ale nic nie sprawi, że będą w stanie wyjść poza granice języka regularnego.

Podstawowa różnica między językiem regularnym a językiem wolnym od kontekstu polega na tym, że język regularny nie zawiera elementów rekurencyjnych. Aby ocenić język rekurencyjny potrzebujesz Push Down Automation aby "pamiętać" gdzie jesteś w rekurencji. NFA / DFA nie przechowuje informacji o stanie, więc nie może zajmij się rekurencją. Więc biorąc pod uwagę definicję języka Nie rekurencyjnego będzie trochę NFA/DFA (ale niekoniecznie praktyczne wyrażenie Regex), aby go opisać.