Jaki jest minimalny koszt połączenia wszystkich wysp?
Istnieje siatka o rozmiarze N X M . Niektóre komórki To Wyspy oznaczone przez "0", a pozostałe to woda . Każda komórka wodna ma numer oznaczający koszt mostu wykonanego na tej komórce. Musisz znaleźć minimalny koszt, za który można podłączyć wszystkie wyspy. Komórka jest połączona z inną komórką, jeśli ma krawędź lub wierzchołek.
Jakiego algorytmu można użyć do rozwiązania tego problemu ?
Edit: co może być użyte jako podejście brute force, jeśli wartości N, M są bardzo małe, powiedzmy NxM
Przykład: na danym obrazku zielone komórki wskazują Wyspy, niebieskie komórki wskazują wodę, a jasnoniebieskie komórki wskazują komórki, na których ma być zbudowany most. Tak więc dla poniższego obrazka odpowiedź będzie 17.

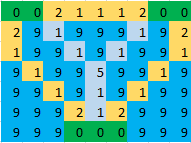
Początkowo myślałem o oznaczeniu wszystkich wysp jako węzłów i połączeniu każdej pary Wysp najkrótszym mostem. Wtedy problem można by zredukować do Minimum, ale w tym podejściu przegapiłem przypadek, w którym krawędzie nakładają się na siebie. na przykład , na poniższym obrazku, Najkrótsza odległość między dowolnymi dwoma wyspami wynosi 7(zaznaczone na Żółto), więc przy użyciu drzew o minimalnej rozpiętości odpowiedź byłaby 14, ale odpowiedź powinna być 11 (oznaczony kolorem jasnoniebieskim).
5 answers
Aby podejść do tego problemu, użyłbym integer programming framework i zdefiniować trzy zestawy zmiennych decyzyjnych:
- x_ij : binarna zmienna wskaĹşnika dla tego, czy budujemy most w miejscu wody (i, j).
- y_ijbcn : binarny wskaĹşnik dla tego, czy lokalizacja wody (i, j) jest n^th lokalizacjÄ… Ĺ‚Ä…czÄ…cÄ… wyspÄ™ b z wyspÄ… c.
- l_bc : binarna zmienna wskaźnika dla tego, czy wyspy b I c są bezpośrednio połączone (aka można chodzić tylko po placach mostowych od b do c).
Dla kosztów budowy mostu c_ij , obiektywna wartość do zminimalizowania wynosi sum_ij c_ij * x_ij. Musimy dodać następujące ograniczenia do modelu:
- musimy upewnić się, że zmienne y_ijbcn są poprawne. Zawsze możemy dotrzeć do placu wodnego tylko wtedy, gdy zbudujemy tam most, więc
y_ijbcn <= x_ijdla każdego miejsca wodnego (i, j). Ponadto,y_ijbc1musi być równe 0, Jeśli (i, j) nie graniczy z wyspą b. wreszcie, dla n > 1,y_ijbcnmoże należy stosować tylko w przypadku, gdy w kroku n-1 użyto sąsiedniej lokalizacji wodnej. DefiniującN(i, j)jako kwadraty wody sąsiadujące (i, j), jest to równoważney_ijbcn <= sum_{(l, m) in N(i, j)} y_lmbc(n-1). - musimy upewnić się, że zmienne l_bc są ustawiane tylko wtedy, gdy B I c są połączone. Jeśli zdefiniujemy
I(c)jako lokalizacje graniczące z wyspą c, można to osiągnąć za pomocąl_bc <= sum_{(i, j) in I(c), n} y_ijbcn. - musimy zapewnić bezpośrednie lub pośrednie powiązanie wszystkich wysp. Można to osiągnąć w następujący sposób: dla każdego niepuste właściwe podzbiory Wysp, wymagają, aby co najmniej jedna wyspa w s była połączona z co najmniej jedną wyspą w dopełniaczu S, którą nazwiemy S'. W ograniczeniach możemy to zaimplementować dodając ograniczenie dla każdego niepustego zbioru S O rozmiarze sum_{b in S} sum_{c in S'} l_bc >= 1.
Dla wystąpienia problemu z wyspami K, kwadratami wody w I określoną maksymalną długością ścieżki N, jest to mieszany model programowania liczb całkowitych ze zmiennymi O(K^2WN) i O(K^2WN + 2^K) ograniczenia. Oczywiście stanie się to trudne, ponieważ rozmiar problemu staje się duży, ale może to być rozwiązywalne dla rozmiarów, na których Ci zależy. Aby poczuć skalowalność, zaimplementuję ją w Pythonie używając pakietu pulp. Zacznijmy od mniejszej mapy 7 x 9 z 3 wyspami na dole pytania: {]}
import itertools
import pulp
water = {(0, 2): 2.0, (0, 3): 1.0, (0, 4): 1.0, (0, 5): 1.0, (0, 6): 2.0,
(1, 0): 2.0, (1, 1): 9.0, (1, 2): 1.0, (1, 3): 9.0, (1, 4): 9.0,
(1, 5): 9.0, (1, 6): 1.0, (1, 7): 9.0, (1, 8): 2.0,
(2, 0): 1.0, (2, 1): 9.0, (2, 2): 9.0, (2, 3): 1.0, (2, 4): 9.0,
(2, 5): 1.0, (2, 6): 9.0, (2, 7): 9.0, (2, 8): 1.0,
(3, 0): 9.0, (3, 1): 1.0, (3, 2): 9.0, (3, 3): 9.0, (3, 4): 5.0,
(3, 5): 9.0, (3, 6): 9.0, (3, 7): 1.0, (3, 8): 9.0,
(4, 0): 9.0, (4, 1): 9.0, (4, 2): 1.0, (4, 3): 9.0, (4, 4): 1.0,
(4, 5): 9.0, (4, 6): 1.0, (4, 7): 9.0, (4, 8): 9.0,
(5, 0): 9.0, (5, 1): 9.0, (5, 2): 9.0, (5, 3): 2.0, (5, 4): 1.0,
(5, 5): 2.0, (5, 6): 9.0, (5, 7): 9.0, (5, 8): 9.0,
(6, 0): 9.0, (6, 1): 9.0, (6, 2): 9.0, (6, 6): 9.0, (6, 7): 9.0,
(6, 8): 9.0}
islands = {0: [(0, 0), (0, 1)], 1: [(0, 7), (0, 8)], 2: [(6, 3), (6, 4), (6, 5)]}
N = 6
# Island borders
iborders = {}
for k in islands:
iborders[k] = {}
for i, j in islands[k]:
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if (i+dx, j+dy) in water:
iborders[k][(i+dx, j+dy)] = True
# Create models with specified variables
x = pulp.LpVariable.dicts("x", water.keys(), lowBound=0, upBound=1, cat=pulp.LpInteger)
pairs = [(b, c) for b in islands for c in islands if b < c]
yvals = []
for i, j in water:
for b, c in pairs:
for n in range(N):
yvals.append((i, j, b, c, n))
y = pulp.LpVariable.dicts("y", yvals, lowBound=0, upBound=1)
l = pulp.LpVariable.dicts("l", pairs, lowBound=0, upBound=1)
mod = pulp.LpProblem("Islands", pulp.LpMinimize)
# Objective
mod += sum([water[k] * x[k] for k in water])
# Valid y
for k in yvals:
i, j, b, c, n = k
mod += y[k] <= x[(i, j)]
if n == 0 and not (i, j) in iborders[b]:
mod += y[k] == 0
elif n > 0:
mod += y[k] <= sum([y[(i+dx, j+dy, b, c, n-1)] for dx in [-1, 0, 1] for dy in [-1, 0, 1] if (i+dx, j+dy) in water])
# Valid l
for b, c in pairs:
mod += l[(b, c)] <= sum([y[(i, j, B, C, n)] for i, j, B, C, n in yvals if (i, j) in iborders[c] and B==b and C==c])
# All islands connected (directly or indirectly)
ikeys = islands.keys()
for size in range(1, len(ikeys)/2+1):
for S in itertools.combinations(ikeys, size):
thisSubset = {m: True for m in S}
Sprime = [m for m in ikeys if not m in thisSubset]
mod += sum([l[(min(b, c), max(b, c))] for b in S for c in Sprime]) >= 1
# Solve and output
mod.solve()
for row in range(min([m[0] for m in water]), max([m[0] for m in water])+1):
for col in range(min([m[1] for m in water]), max([m[1] for m in water])+1):
if (row, col) in water:
if x[(row, col)].value() > 0.999:
print "B",
else:
print "-",
else:
print "I",
print ""
Uruchomienie domyślnego solvera z pakietu pulp (CBC solver) zajmuje 1,4 sekundy i wyświetla prawidłowe rozwiązanie:
I I - - - - - I I
- - B - - - B - -
- - - B - B - - -
- - - - B - - - -
- - - - B - - - -
- - - - B - - - -
- - - I I I - - -
Następna, na początku pytania rozważmy pełny problem, który jest siatką 13 x 14 z 7 wyspami: {]}
water = {(i, j): 1.0 for i in range(13) for j in range(14)}
islands = {0: [(0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)],
1: [(9, 0), (9, 1), (10, 0), (10, 1), (10, 2), (11, 0), (11, 1),
(11, 2), (12, 0)],
2: [(0, 7), (0, 8), (1, 7), (1, 8), (2, 7)],
3: [(7, 7), (8, 6), (8, 7), (8, 8), (9, 7)],
4: [(0, 11), (0, 12), (0, 13), (1, 12)],
5: [(4, 10), (4, 11), (5, 10), (5, 11)],
6: [(11, 8), (11, 9), (11, 13), (12, 8), (12, 9), (12, 10), (12, 11),
(12, 12), (12, 13)]}
for k in islands:
for i, j in islands[k]:
del water[(i, j)]
for i, j in [(10, 7), (10, 8), (10, 9), (10, 10), (10, 11), (10, 12),
(11, 7), (12, 7)]:
water[(i, j)] = 20.0
N = 7
Rozwiązania MIP często stosunkowo szybko uzyskują dobre rozwiązania, a następnie poświęcają dużo czasu na udowodnienie optymalności rozwiązania. Używając tego samego kodu rozwiązującego, co powyżej, program nie kończy się w ciągu 30 minut. Można jednak podać limit czasu do rozwiązania, aby uzyskać przybliżone rozwiązanie:
mod.solve(pulp.solvers.PULP_CBC_CMD(maxSeconds=120))
Daje to rozwiązanie o obiektywnej wartości 17:
I I - - - - - I I - - I I I
I I - - - - - I I - - - I -
I I - - - - - I - B - B - -
- - B - - - B - - - B - - -
- - - B - B - - - - I I - -
- - - - B - - - - - I I - -
- - - - - B - - - - - B - -
- - - - - B - I - - - - B -
- - - - B - I I I - - B - -
I I - B - - - I - - - - B -
I I I - - - - - - - - - - B
I I I - - - - - I I - - - I
I - - - - - - - I I I I I I
Aby poprawić jakość otrzymywanych rozwiązań, możesz użyć komercyjnego solvera MIP (jest to bezpłatne, jeśli jesteś w instytucji akademickiej i prawdopodobnie nie jest wolne w inny sposób). Na przykład, oto wydajność Gurobi 6.0.4, ponownie z limitem czasu 2 minut (choć z dziennika rozwiązania czytamy, że solver znalazł aktualne najlepsze rozwiązanie w ciągu 7 sekund): {]}
mod.solve(pulp.solvers.GUROBI(timeLimit=120))
To rzeczywiście znajduje rozwiązanie o wartości obiektywnej 16, jeden lepszy niż OP był w stanie znajdź ręcznie!
I I - - - - - I I - - I I I
I I - - - - - I I - - - I -
I I - - - - - I - B - B - -
- - B - - - - - - - B - - -
- - - B - - - - - - I I - -
- - - - B - - - - - I I - -
- - - - - B - - B B - - - -
- - - - - B - I - - B - - -
- - - - B - I I I - - B - -
I I - B - - - I - - - - B -
I I I - - - - - - - - - - B
I I I - - - - - I I - - - I
I - - - - - - - I I I I I I
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-10-19 00:25:19
Problem ten jest odmianą drzewa Steinera nazywanego węzłowym drzewem Steinera , specjalizującym się w pewnej klasie Wykresów. Zwięźle, drzewo Steinera ważone węzłami jest, biorąc pod uwagę wykres ważony węzłami, gdzie niektóre węzły są terminalami, Znajdź najtańszy zestaw węzłów obejmujący wszystkie terminale, które indukują podłączony podgraf. Niestety, nie mogę znaleźć żadnych rozwiązań w niektórych pobieżnych wyszukiwaniach.
Aby sformułować jako program integer, stwórz zmienną 0-1 dla każdego węzła spoza terminala, wtedy dla wszystkich podzbiorów węzłów nie-terminalowych, których usunięcie z grafu początkowego rozłącza dwa terminale, wymagane jest, aby suma zmiennych w podzbiorze wynosiła co najmniej 1. Powoduje to zbyt wiele ograniczeń, więc będziesz musiał je leniwie egzekwować, używając wydajnego algorytmu łączności z węzłami (w zasadzie max flow), aby wykryć maksymalnie naruszone ograniczenie. Przepraszamy za brak szczegółów, ale będzie to ból do wdrożenia, nawet jeśli jesteś już zaznajomiony z integer programowanie.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-06-16 17:03:50
Podejście brute-force, w pseudo-kodzie:
start with a horrible "best" answer
given an nxm map,
try all 2^(n*m) combinations of bridge/no-bridge for each cell
if the result is connected, and better than previous best, store it
return best
W C++ można to zapisać jako
// map = linearized map; map[x*n + y] is the equivalent of map2d[y][x]
// nm = n*m
// bridged = true if bridge there, false if not. Also linearized
// nBridged = depth of recursion (= current bridge being considered)
// cost = total cost of bridges in 'bridged'
// best, bestCost = best answer so far. Initialized to "horrible"
void findBestBridges(char map[], int nm,
bool bridged[], int nBridged, int cost, bool best[], int &bestCost) {
if (nBridged == nm) {
if (connected(map, nm, bridged) && cost < bestCost) {
memcpy(best, bridged, nBridged);
bestCost = best;
}
return;
}
if (map[nBridged] != 0) {
// try with a bridge there
bridged[nBridged] = true;
cost += map[nBridged];
// see how it turns out
findBestBridges(map, nm, bridged, nBridged+1, cost, best, bestCost);
// remove bridge for further recursion
bridged[nBridged] = false;
cost -= map[nBridged];
}
// and try without a bridge there
findBestBridges(map, nm, bridged, nBridged+1, cost, best, bestCost);
}
Po wykonaniu pierwszego połączenia (zakładam, że przekształcasz swoje mapy 2d na tablice 1d dla ułatwienia kopiowania), bestCost będzie zawierał koszt najlepszej odpowiedzi, a best będzie zawierał wzór mostów, który ją daje. Jest to jednak niezwykle powolne.
Optymalizacja:
- poprzez użycie "granicy mostu" i uruchomienie algorytmu zwiększania maksimum liczby mostów, można znaleźć Minimalne odpowiedzi bez eksplorowania całego drzewa. Znalezienie odpowiedzi 1-mostowej, gdyby istniała, byłoby O(nm) zamiast O (2^nm) - drastyczna poprawa.
- możesz uniknąć wyszukiwania (zatrzymując rekurencję; jest to również nazywane "przycinaniem") po przekroczeniu
bestCost, ponieważ nie ma sensu szukać dalej. Jeśli nie może być lepiej, nie szukaj dalej. - powyższe przycinanie działa lepiej, jeśli spojrzysz na" dobrych " kandydatów przed spojrzeniem na "złe" (jak to jest, komórki są wyświetlane w kolejności od lewej do prawej, od góry do dołu). Dobrą heurystyką byłoby rozważenie komórek, które znajdują się blisko kilku niepowiązanych składników, jako o wyższym priorytecie niż komórki, które nie są. Jednak po dodaniu heurystyki wyszukiwanie zaczyna przypominać A * (i potrzebujesz też kolejki priorytetów).
- duplikaty mostów i mostów donikąd należy unikać. Każdy most, który nie rozłącza sieci wyspowej, jeśli zostanie usunięty, jest zbędne.
Ogólny algorytm wyszukiwania, taki jak a* pozwala na znacznie szybsze wyszukiwanie, chociaż znalezienie lepszej heurystyki nie jest prostym zadaniem. Jeśli chodzi o podejście bardziej specyficzne dla problemu, najlepszym rozwiązaniem jest użycie istniejących wyników na drzewach Steiner , zgodnie z sugestią @Gassa. Należy jednak pamiętać, że problem budowania drzew Steinera na siatkach ortogonalnych jest NP-kompletny, zgodnie z tym artykułem Gareya i Johnsona .
Jeśli "wystarczająco dobry" wystarczy, genetyczne algorytm może prawdopodobnie szybko znaleźć akceptowalne rozwiązania, o ile dodasz kilka kluczowych heurystyk co do preferowanego położenia mostka.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-06-17 09:46:17
Biorąc pod uwagę, że ten problem ma miejsce w siatce i masz dobrze zdefiniowane parametry, podchodziłbym do problemu z systematyczną eliminacją przestrzeni problemowej poprzez stworzenie minimalnego drzewa rozpiętości. W ten sposób, to ma sens dla mnie, jeśli podejść do tego problemu z algorytmem Prim.
Niestety, teraz napotkasz problem abstrakcji siatki w celu utworzenia zestawu węzłów i krawędzi... ergo prawdziwym problemem tego posta jest Jak skonwertować moją siatkę n x M na {V} i {E}?
Ten proces konwersji jest, na pierwszy rzut oka, prawdopodobnie NP-trudny ze względu na samą liczbę możliwych kombinacji(Załóżmy, że wszystkie koszty drogi wodnej są identyczne). Aby obsłużyć przypadki, w których ścieżki nakładają się na siebie, należy rozważyć utworzenie wirtualnej Wyspy .
Gdy to zrobisz, uruchom algorytm Prim i powinieneś znaleźć optymalne rozwiązanie.
Nie wierzę, że programowanie dynamiczne może być tutaj skutecznie uruchamiane, ponieważ nie ma żadnej obserwowalnej Zasady optymalności. Jeśli znajdziemy minimalny koszt między dwiema wyspami, nie musi to oznaczać, że możemy znaleźć minimalny koszt między tymi dwoma a trzecią wyspą, lub innym podzbiorem wysp, które będą (według mojej definicji znaleźć MST poprzez Prim) połączone.
Jeśli chcesz, aby Kod (pseudo lub inny) przekonwertował Twoją siatkę na zbiór {V} i {E}, wyślij mi prywatną wiadomość, a ja przyjrzę się splataniu implementacji.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-06-16 17:24:42
Zgadzam się, że jest to problem podróżnego sprzedawcy, ale można go brutalnie zmusić n = 7. Oblicz minimalną ścieżkę kosztową między każdą wyspą, a będziesz miał tylko N(n-1)/2 rozwiązania = 21 obliczeń
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-06-08 14:42:12