Obróbka grafiki 3D - jak obliczyć matrycę modelview

Ta odpowiedź jest prawdopodobnie znacznie dłuższa niż powinna być. Przejdź do dołu akapity 2 lub tak, jeśli już rozumiesz większość matematyki macierzy.

Najłatwiej zacząć od spojrzenia na 1-wymiarowy problem. W 1D mamy punkty na linii. Możemy je przeskalować lub przetłumaczyć. Rozważmy trzy punkty i,j, k i macierz transformacji M .

M = [ s t ]
    [ 0 1 ]

i = [1]   j = [-2]   k = [0]
    [1]       [ 1]       [1]

 j     k  i
─┴──┴──┴──┴──┴─
-2 -1  0  1  2

Gdy mnożymy przez M , otrzymujemy:

i' = Mi = [ s t ][ 1] = [ s+t ]
          [ 0 1 ][ 1]   [  1  ]

j' = Mj = [ s t ][-2] = [-2s+t]
          [ 0 1 ][ 1]   [  1  ]

k' = Mk = [ s t ][ 0] = [  t  ]
          [ 0 1 ][ 1]   [  1  ]

Więc jeśli Przypisz wartości s i t, wtedy otrzymamy różne przekształcenia na naszym "trójkącie" 1D. Skalowanie zmienia odległość między "punktami" , podczas gdy czyste tłumaczenie przesuwa je w stosunku do początku, zachowując stałą odstępu:

   s=1 t=0           s=2 t=1           s=1 t=2
 j     k  i        j     k  i        j     k  i   
─┴──┴──┴──┴──┴─   ─┴──┴──┴──┴──┴─   ─┴──┴──┴──┴──┴─
-2 -1  0  1  2    -3 -1  1  3  5     0  1  2  3  4

Ważne jest, aby pamiętać, że kolejność przekształceń jest krytyczna. Te transformacje 1D skalują się i następnie tłumaczą. Gdybyś miał najpierw przetłumaczyć, to "punkt" byłby różną odległością od pochodzenia, a więc czynnik skalowania wpłynie na to inaczej. Z tego powodu przekształcenia są często przechowywane w oddzielnych macierzach, tak że kolejność jest jasna.

Jeśli przeniesiemy się do 2D, otrzymamy macierz N:

   [1 0 tx][ cos(a) sin(a) 0][sx  0 0] [ sx*cos(a) sx*sin(a) tx ]   
N =[0 1 ty][-sin(a) cos(a) 0][ 0 sy 0]=[-sy*sin(a) sy*cos(a) ty ]  
   [0 0 1 ][   0      0    1][ 0  0 1] [    0         0       1 ]

Ta macierz będzie 1) skalowanie punktu przez sx,sy, 2) obróć punkt wokół początku o a stopnie, a następnie 3 Przetłumacz punkt przez tx, ty . Zauważ, że macierz ta jest skonstruowany przy założeniu, że punkty są reprezentowane jako wektory kolumnowe i że mnożenie będzie miało miejsce jako Np. Jak powiedział datenwolf, jeśli chcesz użyć reprezentacji wektorowej wiersza punktów, ale zastosuj tę samą transformację, możesz transponować wszystko i zamienić kolejność. Jest to ogólna właściwość mnożenia macierzy: (AB)^T = (B^T) (A^T) .

To powiedziawszy, możemy mówić o przemianach w kategoriach obiektu, świata i współrzędnych oczu. Jeśli oko siedzi na początku świata, patrząc w dół świata negatywnej osi z, Z +x w prawo i + y w górę, a obiekt, sześcian, siedzi 10 jednostek w dół-z (wyśrodkowany na osi z), o szerokości 2 wzdłuż x świata, głębokość 3 wzdłuż z i wysokość 4 wzdłuż y świata. następnie, jeśli środek sześcianu jest lokalnym ramką odniesienia obiektu i jego lokalne osie wygodnie wyrównują się z osiami świata. Wtedy wierzchołki pola we współrzędnych obiektu są wariantami na [+/-1,+/-2,+/-1.5]^T. Wierzchołek Bliski, górny, prawy (z punktu widzenia oka) ma współrzędne obiektu [1,2,1.5]^T, W współrzędnych świata , ten sam wierzchołek jest [1,2,-8.5]^T (1.5-10=-8.5). Ze względu na to, gdzie jest oko, w którą stronę ono wskazuje, i fakt, że definiujemy nasze oko tak samo jak OpenGL, ten wierzchołek ma te same współrzędne oczu Jak współrzędne świata. Więc przesuńmy i obróćmy oko tak, aby oko X było w prawo (rt) a oko y jest w górę i oko -z jest spójrz (lk) i oko jest umieszczone w [eyeright(ex) eyeup(ey) eyelook(ez)]^T. Ponieważ chcemy przekształcić współrzędne obiektu na współrzędne oczu (co oznacza, że będziemy traktować oko jako źródło), weźmiemy odwrotność tych przekształceń i zastosujemy je do wierzchołków obiektów (po przekształceniu ich w Współrzędne świata). Więc będziemy mieli:

ep = [WORLD_TO_EYE]*[OBJECT_TO_WORLD]*wp;

Dokładniej, dla naszego wierzchołka zainteresowania, będziemy mieć:

[ rt.x  rt.y  rt.z 0][1 0 0 -ex][1 0 0  0 ][ 1 ]
[ up.x  up.y  up.z 0][0 1 0 -ey][0 1 0  0 ][ 2 ]
[-lk.x -lk.y -lk.z 0][0 0 1 -ez][0 0 1 -10][1.5]
[   0     0     0  1][0 0 0  1 ][0 0 0  1 ][ 1 ]

Dla wygody, oddzieliłem tłumaczenie, na które wpływa rotacja oka. Właściwie, teraz, kiedy napisałem tak wiele, może to być punkt zamieszania. Matryca, którą dałeś, obróci się, a następnie przełoży. Założyłem, że tłumaczenie oka jest we współrzędnych świata. Ale jak napisałeś w swoim pytaniu, to faktycznie wykonuje tłumaczenie we współrzędnych oczu. Zanegowałem również lk ponieważ zdefiniowaliśmy oko, aby patrzeć w dół ujemną oś z, ale aby zrobić standardową macierz obrotu, chcemy użyć wartości dodatnich.

W każdym razie, mogę kontynuować, ale może to już odpowiada na twoje pytanie.

Ciąg dalszy:

Wyjaśnienie powyższego nieco dalej, rozdzielenie transformacji oka na dwa składniki znacznie ułatwia znalezienie odwrotności. Łatwo zauważyć, że jeśli tłumaczenie tx przesuwa oko gdzieś w stosunku do obiektów na świecie, możemy utrzymać te same względne pozycje między okiem a punktami na świecie, przesuwając wszystko na świecie o -tx i utrzymując oko w pozycji nieruchomej.

Podobnie, rozważ orientację oka zdefiniowaną przez jego domyślną prawo, up , and look wektory:

     [1]      [0]      [ 0]
d_rt=[0] d_up=[1] d_lk=[ 0]
     [0]      [0]      [-1]

Tworzenie macierzy obrotu, która wskazuje te trzy wektory w nowym kierunku jest łatwe. Po prostu ustawiamy nasze trzy nowe osie rt, do góry, lk (jako wektory kolumnowe):

[rt.x up.x -lk.x 0]
[rt.y up.y -lk.y 0]
[rt.z up.z -lk.z 0]
[  0    0     0  1]

Łatwo zauważyć, że jeśli powiększysz d_rt, d_up i d_lk i pomnożysz przez powyższą macierz, otrzymasz rt, odpowiednio do góry i lk z powrotem. Więc zastosowaliśmy transformację, którą chcieliśmy. Aby mieć prawidłową rotację, trzy wektory muszą być ortonormalne. To tylko zmiana podstaw. Z tego powodu możemy znaleźć odwrotność tej macierzy całkiem wygodnie, przyjmując jej transpozycję. To właśnie zrobiłem. powyżej. Jeśli zastosujesz tę transponowaną matrycę do wszystkich punktów w współrzędnych świata i pozostawisz oko nieruchome, punkty utrzymają tę samą pozycję, względem oka, tak jakby oko się obróciło.

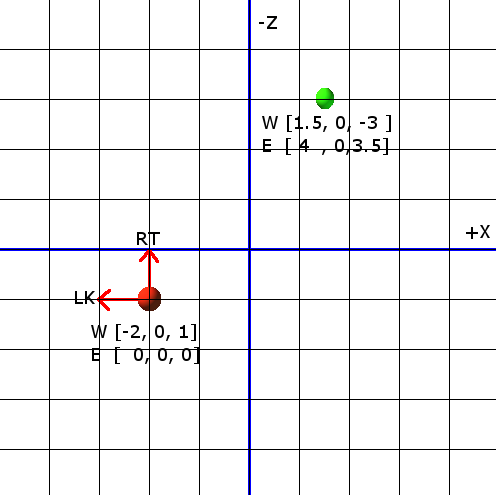
Na Przykład:

Przypisać (w współrzędnych świata):

   [ 0]    [0]    [-1]     [-2]     [1.5]
rt=[ 0] up=[1] lk=[ 0] eye=[ 0] obj=[ 0 ]
   [-1]    [0]    [ 0]     [ 1]     [-3 ]