Wygenerować losowy punkt w okręgu (równomiernie)
Muszę wygenerować jednolicie losowy punkt w okręgu o promieniu R .
Zdaję sobie sprawę, że wybierając jednolicie losowy kąt w przedziale [0 ... 2π), a równomiernie losowy Promień w przedziale (0 ... R ) kończyłbym z większą liczbą punktów w kierunku środka, ponieważ dla dwóch podanych promieni, punkty w mniejszym promieniu będą bliżej siebie niż dla punktów w większym promieniu.
Znalazłem wpis na tym blogu tutaj ale Nie rozumiem jego rozumowania. Przypuszczam, że to prawda, ale naprawdę chciałbym zrozumieć skąd on się bierze (2 / R2)×r i w jaki sposób wyprowadza ostateczne rozwiązanie.
Aktualizacja: 7 lat po opublikowaniu tego pytania nadal nie otrzymałem satysfakcjonującej odpowiedzi na rzeczywiste pytanie dotyczące matematyki za algorytmem pierwiastka kwadratowego. Więc spędziłem dzień pisząc odpowiedź. Link do mojej odpowiedzi.
21 answers
Podejdźmy do tego tak, jak Archimedes.
Jak możemy wygenerować punkt równomiernie w trójkącie ABC, gdzie / AB / =|BC/? Ułatwmy to, rozszerzając do równoległoboku ABCD. W ABCD Łatwo jest generować punkty równomiernie. Jednolicie wybieramy losowy punkt X NA AB i Y NA BC i wybieramy Z taki, że xbyz jest równoległobokiem. Aby uzyskać jednolicie wybrany punkt w oryginalnym trójkącie, po prostu spasujemy wszystkie punkty, które pojawiają się w ADC z powrotem do ABC wzdłuż AC.
Teraz rozważ koło. W granicy możemy myśleć o niej jako o nieskończenie wielu izocelach trójkątów ABC z B na początku i A I C na obwodzie znikają blisko siebie. Możemy wybrać jeden z tych trójkątów po prostu wybierając kąt theta. Więc teraz musimy wygenerować odległość od centrum, wybierając punkt w skrawku ABC. Ponownie, Rozszerz do ABCD, gdzie D jest teraz dwa razy promień od środka okręgu.
Wybranie przypadkowego punktu w ABCD jest łatwe przy użyciu powyższej metody. Wybierz losowy punkt na AB. / Align = "left" / Ie. wybierz parę liczb losowych X i y równomiernie na [0, R] podając odległości od środka. Nasz trójkąt jest cienki, więc AB i BC są zasadniczo równoległe. Więc punkt Z jest po prostu odległością x + y Od początku. Jeśli x + y > R składamy z powrotem.
Oto kompletny algorytm dla R = 1. Mam nadzieję, że się zgodzisz, że to proste. Używa trig, ale możesz dać gwarancję, jak długo to zajmie i ile random() połączeń potrzebuje, w przeciwieństwie do próby odrzucenia.
t = 2*pi*random()
u = random()+random()
r = if u>1 then 2-u else u
[r*cos(t), r*sin(t)]
f[] := Block[{u, t, r},
u = Random[] + Random[];
t = Random[] 2 Pi;
r = If[u > 1, 2 - u, u];
{r Cos[t], r Sin[t]}
]
ListPlot[Table[f[], {10000}], AspectRatio -> Automatic]
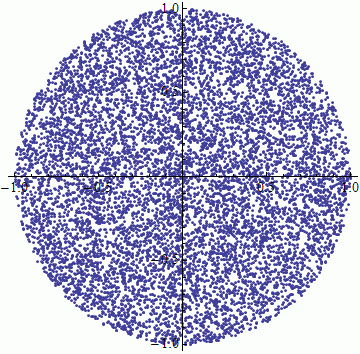
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2011-05-01 15:15:12
Jak wygenerować losowy punkt w okręgu o promieniu R :
r = R * sqrt(random())
theta = random() * 2 * PI
(zakładając, że random() daje wartość z zakresu od 0 do 10)
Jeśli chcesz przekonwertować to na współrzędne kartezjańskie, możesz zrobić
x = r * cos(theta)
y = r * sin(theta)
Dlaczego sqrt(random())?
Przyjrzyjmy się matematyce, która prowadzi do sqrt(random()). Załóżmy dla uproszczenia, że pracujemy z okręgiem jednostkowym, tzn. R = 1.
Średnia odległość między punktami powinna być taka sama niezależnie jak daleko od centrum patrzymy. Oznacza to na przykład, że patrząc na obwód okręgu o obwodzie 2 powinniśmy znaleźć dwa razy więcej punktów niż liczba punktów na obwodzie okręgu o obwodzie 1.

Ponieważ obwód okręgu (2πr) rośnie liniowo z r , wynika z tego, że liczba przypadkowych punktów powinna rosnąć liniowo z r. Innymi słowy, pożądany funkcja gęstości prawdopodobieństwa (PDF) rośnie liniowo. Ponieważ plik PDF powinien mieć obszar równy 1, A Maksymalny promień wynosi 1, Mamy

Używamy triku o nazwie próbkowanie odwrotnej transformacji
- Z PDF, tworzenie funkcja rozkładu kumulacyjnego (CDF)
- Mirror this along y = x
- Zastosuj wynikowä ... funkcjÄ ™ do jednorodnej wartoĹ " ci pomiÄ ™ dzy 0 a 1.
Załóżmy, że chcemy wygenerować losowy punkt o następującym rozkładzie:
To jest
- 1/5 punktów równomiernie pomiędzy 1 i 2 oraz
- 4/5 punktów równomiernie między 2 a 3.
CDF jest, jak sama nazwa wskazuje, zbiorczą wersją PDF. Intuicyjnie: podczas gdy PDF (x) opisuje liczbę losowych wartości W x , CDF(x) opisuje liczbę losowych wartości mniejszą niż x.
W tym przypadku CDF wyglądałby następująco:
Aby zobaczyć jak jest to przydatne, wyobraź sobie, że strzelamy kulami od lewej do prawej na równomiernie rozłożonych wysokościach. Kiedy kule trafiają w linię, spadają na ziemię: {]}
[9]} Zobacz, jak gęstość pocisków na ziemi odpowiada naszemu pożądanemu rozkładowi! Już prawie jesteśmy!
Problem polega na tym, że dla tej funkcji oś y jest wyjściem , a oś x jest wejściem. Możemy tylko " strzelać kulami prosto z ziemi"! Potrzebujemy funkcji odwrotnej!
Dlatego odzwierciedlamy całość; x staje się y i y staje się x :
Nazywamy to CDF-1. Aby uzyskać wartości zgodnie z żądaną dystrybucją, używamy CDF-1(random()).
...wracając więc do generowania losowych wartości promienia, gdzie nasz PDF jest równy 2x.
Krok 1: Utwórz CDF:
Ponieważ pracujemy z reals, CDF jest wyrażony jako integralność pliku PDF.
CDF(x) = ∫ 2x = x2
Krok 2: Lustro CDF wzdłuż y = x:
Matematycznie sprowadza się to do zamiany x i y i rozwiązania dla y:
CDF: y = x2
Swap: x = y2
Rozwiąż: y = √x
CDF-1: y = √x
Krok 3: Zastosuj wynikową funkcję do jednolitej wartości między 0 a 1
CDF-1(random ()) = √random ()
Czyli to co postanowiliśmy wyprowadzić : -)
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2018-06-20 20:43:04
Oto szybkie i proste rozwiązanie.
Wybierz dwie liczby losowe z zakresu (0, 1), a mianowicie a i b. Jeśli b < a, zamień je. Masz na myśli (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)).
Możesz pomyśleć o tym rozwiązaniu w następujący sposób. Gdybyś wziął okrąg, wyciął go, a potem wyprostował, otrzymałbyś trójkąt pod kątem prostym. Przeskaluj ten trójkąt w dół, a będziesz miał Trójkąt od (0, 0) do (1, 0) do (1, 1) i z powrotem do (0, 0). Wszystkie te przekształcenia zmieniają gęstość równomiernie. Co masz zrobione jest jednolicie wybrany losowy punkt w trójkącie i odwrócił proces, aby uzyskać punkt w okręgu.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2011-04-30 02:07:28
Zwróć uwagę na gęstość punktu proporcjonalną do odwrotnego kwadratu promienia, stąd zamiast wybrać r z [0, r_max], Wybierz z [0, r_max^2], a następnie Oblicz współrzędne jako:
x = sqrt(r) * cos(angle)
y = sqrt(r) * sin(angle)
To da ci równomierny rozkład punktów na dysku.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2016-01-28 15:50:56
Pomyśl o tym w ten sposób. Jeśli masz prostokąt, w którym jedna oś to promień, a jedna to kąt, i bierzesz punkty wewnątrz tego prostokąta, które są w pobliżu promienia 0. Wszystkie te spadną bardzo blisko źródła (czyli blisko siebie na okręgu.) Jednak punkty w pobliżu promienia R, wszystkie te spadną w pobliżu krawędzi okręgu (czyli daleko od siebie.)
To może dać ci jakiś pomysł, dlaczego masz takie zachowanie.
Czynnik, który jest pochodną ten link mówi, ile odpowiedniego obszaru w prostokącie należy dostosować, aby nie zależał od promienia po odwzorowaniu go na okrąg.
Edit: więc to, co pisze w linku, który udostępniasz, jest, " łatwo to zrobić, obliczając odwrotność rozkładu kumulacyjnego, i otrzymujemy dla r:".
Podstawowym założeniem jest tutaj, że można utworzyć zmienną o pożądanym rozkładzie z uniformu poprzez odwzorowanie uniformu za pomocą funkcji odwrotnej kumulacji funkcja rozkładu pożądanej funkcji gęstości prawdopodobieństwa. Dlaczego? Na razie Uznaj to za pewnik, ale to jest fakt.
Oto moje intuicyjne Wyjaśnienie matematyki. Funkcja gęstości f (r) w odniesieniu do r musi być proporcjonalna do samego r. Zrozumienie tego faktu jest częścią wszelkich podstawowych książek rachunkowych. Zobacz sekcje dotyczące elementów biegunowych. Niektóre inne plakaty wspominały o tym.
Więc nazwiemy to f (r) = C * r;
To okazuje się być Większość praca. Teraz, ponieważ f (r) powinno być gęstością prawdopodobieństwa, można łatwo zauważyć, że integrując f (r) w przedziale (0,R) otrzymujesz, że C = 2 / R^2 (jest to ćwiczenie dla czytelnika.)
Zatem f(r) = 2*r/R^2
OK, więc tak masz formułę w linku.
Następnie, końcowa część idzie z jednorodnej zmiennej losowej u w (0,1) musisz odwzorować przez funkcję odwrotną funkcji rozkładu kumulacyjnego z tej pożądanej gęstości f (r). Zrozumieć dlaczego tak jest, musisz znaleźć zaawansowany tekst prawdopodobieństwa, taki jak Papoulis prawdopodobnie (lub wyprowadzić go samodzielnie.)
Integrując f(r) otrzymujesz F (r) = R^2 / R^2
Aby znaleźć funkcję odwrotną tego należy ustawić u = R^2/R^2 i następnie rozwiązać dla r, co daje r = r * sqrt (u)
To też ma sens intuicyjnie, u = 0 powinno być odwzorowane na r = 0. Również, u = 1 shoudl map do r = R. również, przechodzi przez funkcję pierwiastka kwadratowego, co ma sens i pasuje do łącza.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2011-04-30 11:45:51
To naprawdę zależy od tego, co masz na myśli przez "jednolicie przypadkowe". Jest to subtelny punkt i możesz przeczytać więcej na ten temat na stronie wiki tutaj: http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29 , Gdzie ten sam problem, dając różne interpretacje "jednolicie przypadkowych" daje różne odpowiedzi!
W zależności od tego, jak wybierzesz punkty, rozkład może się różnić, nawet jeśli są one jednolicie losowe w pewnym sensie.
Wygląda na to, że blog wpis stara się uczynić go równomiernie losowym w następującym sensie: jeśli weźmiemy podokręg okręgu o tym samym środku, to prawdopodobieństwo, że punkt spadnie w tym regionie jest proporcjonalne do obszaru regionu. To, jak sądzę, próbuje podążać za obecnie standardową interpretacją "równomiernie losowego" dla regionów 2D z obszarów zdefiniowanych na nich : prawdopodobieństwo punktu padającego w dowolnym regionie (z obszarem dobrze zdefiniowanym) jest proporcjonalne do obszaru tego regionu.
Naiwne rozwiązanie nie działa, ponieważ daje większą gęstość prawdopodobieństwa punktom bliżej środka okręgu. Innymi słowy okrąg, który ma promień r/2 ma prawdopodobieństwo r / 2 uzyskania w nim wybranego punktu, ale ma obszar (liczbę punktów) pi*r^2/4.
Dlatego chcemy, aby gęstość prawdopodobieństwa promienia miała następującą własność:
Prawdopodobieństwo wyboru promienia mniejszego lub równego danemu r musi być proporcjonalne do powierzchni okrąg o promieniu r. (ponieważ chcemy mieć równomierny rozkład na punktach i większe obszary oznaczają więcej punktów)
Innymi słowy chcemy, aby prawdopodobieństwo wyboru promienia pomiędzy [0, r] było równe jego udziałowi w ogólnej powierzchni okręgu. Całkowita powierzchnia okręgu to pi * R^2, a powierzchnia okręgu o promieniu r to pi * r^2. Dlatego chcielibyśmy, aby prawdopodobieństwo wyboru promienia między [0, r] było (pi * r^2)/(pi*R^2) = r^2 / R^2.
Teraz przychodzi matematyka:
Prawdopodobieństwo wyboru promienia pomiędzy [0, r] jest całką P (R) dr od 0 do r (to tylko dlatego, że dodajemy wszystkie prawdopodobieństwa mniejszych promieni). Tak więc chcemy całki (p (R) dr) = r^2/R^2. Możemy wyraźnie zobaczyć, że R^2 jest stałą, więc wszystko, co musimy zrobić, to dowiedzieć się, które p (r), gdy zintegrowane dałoby nam coś takiego jak R^2. Odpowiedź jest wyraźnie stała r*. Całka (r * stała dr) = R^2/2 * stała. Musi być równa r^2/R^2, a więc stała = 2 / R^2. Zatem masz rozkład prawdopodobieństwa p (r) = r * 2 / R^2
Uwaga: innym bardziej intuicyjnym sposobem myślenia o problemie jest wyobrażenie sobie, że próbujesz nadać każdemu kołu o promieniu r gęstość prawdopodobieństwa równą proporcji liczby punktów, które ma na swoim obwodzie. Tak więc okrąg, który ma promień R, będzie miał 2 * pi * r "punkty" na swoim obwodzie. Łączna liczba punktów to pi * R^2. Zatem należy dać okrąg r prawdopodobieństwo równe (2 * pi * r) / (pi * R^2) = 2 * r / R^2. Jest to znacznie łatwiejsze do zrozumienia i bardziej intuicyjne, ale nie jest tak matematycznie brzmiące.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2014-07-15 09:05:30
Oto Mój kod Pythona do generowania num losowych punktów z okręgu o promieniu rad:
import matplotlib.pyplot as plt
import numpy as np
rad = 10
num = 1000
t = np.random.uniform(0.0, 2.0*np.pi, num)
r = rad * np.sqrt(np.random.uniform(0.0, 1.0, num))
x = r * np.cos(t)
y = r * np.sin(t)
plt.plot(x, y, "ro", ms=1)
plt.axis([-15, 15, -15, 15])
plt.show()
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2016-02-24 12:31:55
Niech ρ (Promień) i φ (azymut) będą dwiema zmiennymi losowymi odpowiadającymi współrzędnych biegunowych dowolnego punktu wewnątrz okręgu. Jeśli punkty są równomiernie rozłożone, to jaka jest funkcja disribution ρ i φ?
Dla dowolnego r: 0
P [ρ 2
Gdzie S1 i S0 są odpowiednio obszarami okręgu o promieniu R i R. Więc CDF można podać jako:
0 if r<=0
CDF = (r/R)**2 if 0 < r <= R
1 if r > R
I PDF:
PDF = d/dr(CDF) = 2 * (r/R**2) (0 < r <= R).
Zauważ, że dla R = 1 zmienna losowa sqrt (X), gdzie X jest jednorodne na [0, 1) ma dokładnie taki CDF (ponieważ P[sqrt(x)
Rozkład φ jest oczywiście jednorodny od 0 do 2*π. Teraz możesz tworzyć losowe współrzędne biegunowe i konwertować je na kartezjańskie za pomocą równań trygonometrycznych:
x = ρ * cos(φ)
y = ρ * sin(φ)
Nie mogę się oprzeć dodaniu kodu Pythona dla R = 1.
from matplotlib import pyplot as plt
import numpy as np
rho = np.sqrt(np.random.uniform(0, 1, 5000))
phi = np.random.uniform(0, 2*np.pi, 5000)
x = rho * np.cos(phi)
y = rho * np.sin(phi)
plt.scatter(x, y, s = 4)
Będziesz get

Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2018-01-17 19:05:40
Rozwiązanie w Javie i przykład dystrybucji (2000 punktów)
public void getRandomPointInCircle() {
double t = 2 * Math.PI * Math.random();
double r = Math.sqrt(Math.random());
double x = r * Math.cos(t);
double y = r * Math.sin(t);
System.out.println(x);
System.out.println(y);
}
Na podstawie rozwiązania previusa https://stackoverflow.com/a/5838055/5224246 from @ sigfpe
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-06-12 21:20:01
Myślę, że w tym przypadku używanie współrzędnych biegunowych jest sposobem komplikowania problemu, byłoby znacznie łatwiej, jeśli wybierzesz losowe punkty na kwadrat o bokach długości 2R, a następnie wybierz punkty (x,y) takie, że x^2+y^2<=R^2.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2018-06-08 00:59:55
Najpierw generujemy cdf [x] czyli
Prawdopodobieństwo, że punkt jest mniejszy niż odległość x od środka okręgu. Załóżmy, że okrąg ma promień R.
Oczywiście jeśli x jest zerem to cdf[0] = 0
Oczywiście jeśli x jest R to cdf [R] = 1
Oczywiście jeśli x = r to cdf[r] = (Pi r^2) / (Pi R^2)
Dzieje się tak dlatego, że każdy "mały obszar" na okręgu ma takie samo prawdopodobieństwo wybrania, więc prawdopodobieństwo jest proporcjonalne do obszaru w pytanie. A obszar podany odległości x od środka okręgu to Pi R^2
Więc cdf [x] = x^2 / R^2 ponieważ Pi anulują się nawzajem
Mamy cdf [x]=x^2 / R^2 gdzie x przechodzi od 0 do R
Więc rozwiązujemy dla x
R^2 cdf[x] = x^2
x = R Sqrt[ cdf[x] ]
Możemy teraz zastąpić cdf losową liczbą od 0 do 1
x = R Sqrt[ RandomReal[{0,1}] ]
Wreszcie
r = R Sqrt[ RandomReal[{0,1}] ];
theta = 360 deg * RandomReal[{0,1}];
{r,theta}
Otrzymujemy współrzędne biegunowe {0.601168 R, 311.915 deg}
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-12-13 04:24:37
Istnieje liniowa zależność między promieniem a liczbą punktów "w pobliżu" tego promienia, więc musi on użyć rozkładu promienia, który sprawia, że liczba punktów danych w pobliżu promienia r jest proporcjonalna do r.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2011-04-29 21:34:44
Kiedyś użyłem tej metody: Może to być całkowicie nieoptymalizowane (tj. używa tablicy punktu, więc jego bezużyteczne dla dużych okręgów), ale daje losowy rozkład wystarczająco. Możesz pominąć tworzenie macierzy i narysować bezpośrednio, jeśli chcesz. Metoda polega na losowaniu wszystkich punktów w prostokącie, które mieszczą się wewnątrz okręgu.
bool[,] getMatrix(System.Drawing.Rectangle r) {
bool[,] matrix = new bool[r.Width, r.Height];
return matrix;
}
void fillMatrix(ref bool[,] matrix, Vector center) {
double radius = center.X;
Random r = new Random();
for (int y = 0; y < matrix.GetLength(0); y++) {
for (int x = 0; x < matrix.GetLength(1); x++)
{
double distance = (center - new Vector(x, y)).Length;
if (distance < radius) {
matrix[x, y] = r.NextDouble() > 0.5;
}
}
}
}
private void drawMatrix(Vector centerPoint, double radius, bool[,] matrix) {
var g = this.CreateGraphics();
Bitmap pixel = new Bitmap(1,1);
pixel.SetPixel(0, 0, Color.Black);
for (int y = 0; y < matrix.GetLength(0); y++)
{
for (int x = 0; x < matrix.GetLength(1); x++)
{
if (matrix[x, y]) {
g.DrawImage(pixel, new PointF((float)(centerPoint.X - radius + x), (float)(centerPoint.Y - radius + y)));
}
}
}
g.Dispose();
}
private void button1_Click(object sender, EventArgs e)
{
System.Drawing.Rectangle r = new System.Drawing.Rectangle(100,100,200,200);
double radius = r.Width / 2;
Vector center = new Vector(r.Left + radius, r.Top + radius);
Vector normalizedCenter = new Vector(radius, radius);
bool[,] matrix = getMatrix(r);
fillMatrix(ref matrix, normalizedCenter);
drawMatrix(center, radius, matrix);
}
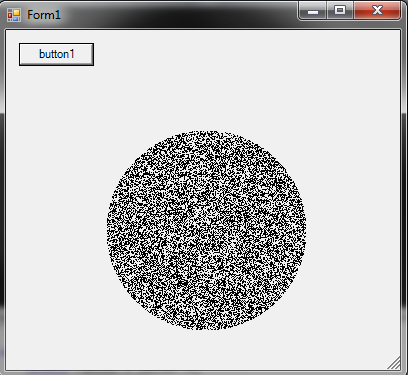
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2011-04-29 22:27:23
Element obszaru w okręgu to dA = rdr*dphi. Ten dodatkowy czynnik R zniszczył twój pomysł, aby losowo wybrać r i phi. Podczas gdy phi jest rozłożone płasko, r nie jest, ale płaskie w 1 / r (tj. jesteś bardziej narażony na uderzenie granicy niż "oko w dziesiątkę").
Więc aby wygenerować punkty równomiernie rozłożone na okręgu wybierz phi z rozkładu płaskiego i r z rozkładu 1 / R.
Alternatywnie należy zastosować metodę Monte Carlo zaproponowaną przez Mehrdada.
EDIT
To wybierz losowe mieszkanie r W 1/r możesz wybrać losowe x z przedziału [1/R, nieskończoność] i obliczyć r=1/x. r jest następnie rozkładane płasko w 1 / R.
Aby obliczyć losowe phi wybierz losowe x z przedziału [0, 1] i Oblicz phi=2*pi * x.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2011-04-29 22:49:12
Nie wiem, czy to pytanie jest nadal otwarte na nowe rozwiązanie z odpowiedziami już udzielonymi, ale zdarzyło mi się, że sam stanąłem przed dokładnie tym samym pytaniem. Próbowałem "rozmyślać" z sobą o rozwiązaniu i znalazłem jedno. To może być to samo, co niektórzy już sugerowali tutaj, ale w każdym razie tutaj jest:
Aby dwa elementy powierzchni okręgu były równe, zakładając równe dr, musimy mieć dtheta1/dtheta2 = r2 / r1. Pisanie wyrażenia prawdopodobieństwa dla ten element jako P(R, theta) = P{ R1
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2013-05-14 21:09:59
Rozwiązanie programistyczne:
- utwórz mapę bitową (macierz wartości logicznych). Może być tak duży, jak chcesz.
- narysuj okrąg na tej mapie bitowej.
- Utwórz tabelę wyszukiwania punktów okręgu.
- Wybierz losowy indeks w tej tabeli wyszukiwania.
const int RADIUS = 64;
const int MATRIX_SIZE = RADIUS * 2;
bool matrix[MATRIX_SIZE][MATRIX_SIZE] = {0};
struct Point { int x; int y; };
Point lookupTable[MATRIX_SIZE * MATRIX_SIZE];
void init()
{
int numberOfOnBits = 0;
for (int x = 0 ; x < MATRIX_SIZE ; ++x)
{
for (int y = 0 ; y < MATRIX_SIZE ; ++y)
{
if (x * x + y * y < RADIUS * RADIUS)
{
matrix[x][y] = true;
loopUpTable[numberOfOnBits].x = x;
loopUpTable[numberOfOnBits].y = y;
++numberOfOnBits;
} // if
} // for
} // for
} // ()
Point choose()
{
int randomIndex = randomInt(numberOfBits);
return loopUpTable[randomIndex];
} // ()
Bitmapa jest potrzebna tylko do wyjaśnienia logiki. Jest to kod bez bitmapy:
const int RADIUS = 64;
const int MATRIX_SIZE = RADIUS * 2;
struct Point { int x; int y; };
Point lookupTable[MATRIX_SIZE * MATRIX_SIZE];
void init()
{
int numberOfOnBits = 0;
for (int x = 0 ; x < MATRIX_SIZE ; ++x)
{
for (int y = 0 ; y < MATRIX_SIZE ; ++y)
{
if (x * x + y * y < RADIUS * RADIUS)
{
loopUpTable[numberOfOnBits].x = x;
loopUpTable[numberOfOnBits].y = y;
++numberOfOnBits;
} // if
} // for
} // for
} // ()
Point choose()
{
int randomIndex = randomInt(numberOfBits);
return loopUpTable[randomIndex];
} // ()
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2015-06-12 03:49:56
Nadal nie jestem pewien dokładnego "(2 / R2)×r", ale to, co jest oczywiste, to liczba punktów wymaganych do rozłożenia w danej jednostce "dr", tzn. wzrost r będzie proporcjonalny do r2, a nie R.
Sprawdź w ten sposób...liczba punktów pod pewnym kątem theta i między r (0,1 R do 0,2 r) tzn. ułamek r i liczba punktów między r (0,6 R do 0,7 R) będzie równa, jeśli użyjesz generacji standardowej, ponieważ różnica wynosi tylko 0,1 R między dwoma przedziałami. ale ponieważ obszar objęty między punktami (0.6 R do 0.7 R) będzie znacznie większy niż obszar pokryty między 0.1 R do 0.2 r, równa liczba punktów będzie słabo rozmieszczone w większym obszarze, to zakładam, że już wiesz, więc funkcja generowania punktów losowych nie może być liniowa, ale kwadratowa, (ponieważ liczba punktów wymaganych do rozłożenia w danej jednostce 'dr', tzn. wzrost r będzie proporcjonalny do r2, a nie R), więc w tym przypadku będzie odwrotna kwadratowa, ponieważ delta mamy (0.1 R) w obu odstępach musi być kwadratem jakiejś funkcji, więc może działać jako wartość nasienna dla liniowego generowania punktów (ponieważ po słowach, to ziarno jest używane liniowo w funkcji Sin i cos), więc wiemy, że dr musi być wartością kwadratową i aby to ziarno było kwadratowe, musimy wywodzić te wartości z pierwiastka kwadratowego z r, a nie z samego r, mam nadzieję, że to czyni to trochę bardziej jasnym.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-01-17 07:16:54
Fajny problem.
Uzasadnienie prawdopodobieństwa wyboru punktu w miarę wzrostu odległości od punktu początkowego zostało wyjaśnione wielokrotnie powyżej. Wyjaśniamy to, biorąc korzeń U [0,1].
Oto ogólne rozwiązanie dla dodatniego r w Pythonie 3.
import numpy
import math
import matplotlib.pyplot as plt
def sq_point_in_circle(r):
"""
Generate a random point in an r radius circle
centered around the start of the axis
"""
t = 2*math.pi*numpy.random.uniform()
R = (numpy.random.uniform(0,1) ** 0.5) * r
return(R*math.cos(t), R*math.sin(t))
R = 200 # Radius
N = 1000 # Samples
points = numpy.array([sq_point_in_circle(R) for i in range(N)])
plt.scatter(points[:, 0], points[:,1])
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2018-06-05 04:55:00
Możesz również użyć swojej intuicji.
Powierzchnia okręgu to pi*r^2
Dla r=1
To daje nam obszar pi. Załóżmy, że mamy jakąś funkcję f, która równomiernie rozdzielałaby N=10 punkty wewnątrz okręgu. Stosunek tutaj jest 10 / pi
Teraz podwajamy obszar i liczbę punktów
Dla r=2 i N=20
To daje obszar 4pi, a stosunek wynosi teraz 20/4pi lub 10/2pi. Stosunek będzie mniejszy i mniejszy im większy promień, ponieważ jego wzrost jest kwadratowy, a N skaluje się liniowo.
Aby to naprawić możemy po prostu powiedzieć
x = r^2
sqrt(x) = r
Jeśli wygenerujesz wektor o współrzędnych biegunowych w ten sposób
length = random_0_1();
angle = random_0_2pi();
Więcej punktów wylądowałoby wokół środka.
length = sqrt(random_0_1());
angle = random_0_2pi();
length nie jest już równomiernie rozłożony, ale wektor będzie teraz równomiernie rozłożony.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2018-07-13 22:11:20
1) Wybierz losowy X pomiędzy -1 i 1.
var X:Number = Math.random() * 2 - 1;
2) Korzystając ze wzoru okręgu, Oblicz maksymalne i minimalne wartości Y, biorąc pod uwagę, że X i promień 1:
var YMin:Number = -Math.sqrt(1 - X * X);
var YMax:Number = Math.sqrt(1 - X * X);
3) Wybierz losowe Y między tymi skrajnościami:
var Y:Number = Math.random() * (YMax - YMin) + YMin;
4) Włącz swoje położenie i promień wartości w końcowej wartości:
var finalX:Number = X * radius + pos.x;
var finalY:Number = Y * radois + pos.y;
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2014-01-21 01:35:28





