Dlaczego sortowanie merge jest najgorszym czasem uruchamiania O (N log n)?

Sortowanie Merge użyj metody dzielenia i podbierania, aby rozwiązać problem sortowania. Po pierwsze, dzieli wejście na pół używając rekurencji. Po podzieleniu sortuje połówki i łączy je w jedno posortowane wyjście. Zobacz rysunek

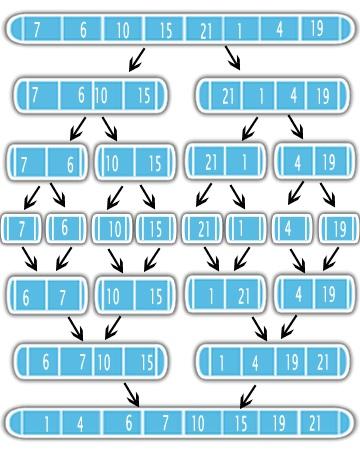
Oznacza to, że lepiej jest najpierw posortować połowę problemu i wykonać prosty podprogram scalania. Dlatego ważne jest, aby znać złożoność podprogramu merge i ile razy będzie on wywoływany w rekurencja.

Pseudo-kod dla sortowania merge jest naprawdę prosty.

# C = output [length = N]
# A 1st sorted half [N/2]
# B 2nd sorted half [N/2]
i = j = 1
for k = 1 to n
    if A[i] < B[j]
        C[k] = A[i]
        i++
    else
        C[k] = B[j]
        j++

Łatwo zauważyć, że w każdej pętli będziesz miał 4 operacje: k++, i++ lub j++, twierdzenie ifi atrybucja C = A|B . Więc będziesz miał mniej lub równą 4N + 2 operacji dających O(N) złożoność. Ze względu na dowód 4N + 2 będzie traktowane jako 6N, ponieważ jest prawdziwe dla N = 1 (4N +2 ).

Więc załóżmy masz wejście z N elementów i założyć N jest potęgą 2. Na każdym poziomie masz dwa razy więcej podproblemów z wejściem z pół elementami z poprzedniego wejścia. Oznacza to, że na poziomie j = 0, 1, 2, ..., lgN będzie 2^j podproblemów z wejściem długości N / 2^j. Liczba operacji na każdym poziomie j będzie mniejsza lub równa

2^j * 6 (N / 2^j) = 6N

Zauważ, że to nie ma znaczenia poziom zawsze będziesz miał mniej lub równe operacje 6N.

Ponieważ istnieją poziomy lgN + 1, złożoność będzie

O (6N *(lgN + 1)) = O(6N*lgN + 6N) = O (N lgN)

Bibliografia:

• algorytmy kursu Coursera: Projektowanie i analiza, Część 1

Dzieje się tak dlatego, że czy jest to najgorszy czy średni przypadek, sortowanie scalające po prostu dzieli tablicę na dwie połówki na każdym etapie, co daje jej LG (n) składnik, a drugi N składnik pochodzi z jego porównań, które są dokonywane na każdym etapie. Tak więc połączenie staje się prawie O (nlg n). Bez względu na to, czy jest to średni czy najgorszy przypadek, współczynnik lg(n) jest zawsze obecny. Współczynnik Rest N zależy od dokonanych porównań, które pochodzą z porównań dokonanych w obu przypadkach. Teraz najgorszy przypadek to taki, w którym N porównania mają miejsce dla N wejścia na każdym etapie. Staje się więc O (nlg n).

Po podzieleniu tablicy na scenę, w której masz pojedyncze elementy tzn. nazwij je podlistami,

• Na każdym etapie porównujemy elementy każdej sublisty z jej sąsiednią sublistą. Na przykład [ponowne wykorzystanie obrazu @Davi ]

  

  1. na etapie-1 każdy element jest porównywany z sąsiednim, więc N / 2 porównań.
  2. na etapie-2 każdy element sublisty jest porównywany z sąsiednią sublistą, ponieważ każda sublista jest posortowana, oznacza to, że Maksymalna liczba porównań dokonanych między dwoma podlistami wynosi n/2
  3. jak zauważyłeś, całkowita liczba etapów będzie log(n) base 2 Więc całkowita złożoność byłaby = = (Maksymalna liczba porównań na każdym etapie * liczba etapów) = = O ((n/2) * log (n)) = = > O(nlog (n))

Algorytm MergeSort wykonuje trzy kroki:

1. Divide krok oblicza pozycję środkową tablicy i zajmuje stały czas O(1).
2. Conquer krok rekurencyjnie sortuje dwie tablice po ok. n / 2 elementy każda.
3. Combine step Scala sumę n elementów przy każdym przejściu wymagającym co najwyżej n porównań, więc zajmuje O (n).

Algorytm wymaga ok. logn do sortowania tablicy N elementów, więc całkowita złożoność czasowa wynosi nlogn.

Wiele innych odpowiedzi jest świetnych, ale nie widziałem żadnej wzmianki o height i depth związanej z przykładami "merge-sort tree". Oto inny sposób podejścia do pytania z dużym naciskiem na drzewo. Oto kolejny obrazek, który pomoże wyjaśnić:

Tylko podsumowanie: jak zauważyły inne odpowiedzi wiemy, że praca łączenia dwóch posortowanych plastrów sekwencji przebiega w czasie liniowym (funkcja merge helper, którą wywołujemy z głównego funkcja sortowania).
Teraz patrząc na to drzewo, w którym możemy myśleć o każdym potomku korzenia (innym niż korzeń) jako rekurencyjnym wywołaniu funkcji sortowania, spróbujmy ocenić, ile czasu spędzamy na każdym węźle... Ponieważ wycinanie sekwencji i scalanie (oba razem) zajmują czas liniowy, czas działania dowolnego węzła jest liniowy w odniesieniu do długości sekwencji w tym węźle.

Tutaj pojawia się głębia drzewa. Jeśli n jest całkowitą wielkością sekwencji oryginalnej, rozmiar sekwencji w dowolnym węźle to n / 2 ⁱ , gdzie i jest głębokością. Jest to pokazane na powyższym obrazku. Zestawiając to razem z liniową ilością pracy dla każdego kawałka, mamy czas pracy O (n / 2 ⁱ ) dla każdego węzła w drzewie. Teraz musimy to podsumować dla węzłów N. Jednym ze sposobów na to jest rozpoznanie, że na każdym poziomie głębokości w drzewie znajdują się 2ⁱ węzły. Więc dla dowolnego poziomu mamy O (2ⁱ * N / 2 ⁱ ), czyli O( n) ponieważ możemy anulować 2ⁱ s! Jeśli każda głębokość jest O (n), musimy po prostu pomnożyć ją przez Wysokość tego binarnego drzewa, którym jest logn. Odpowiedź: O (nlogn)

Reference: struktury danych i algorytmy w Pythonie

Algorytm merge-sort sortuje sekwencję S O rozmiarze N W O (N log n) czas, zakładając, że dwa elementy S można porównać w czasie O(1).

Drzewo rekurencyjne będzie miało głębokość log(N), a na każdym poziomie w tym drzewie wykonasz połączoną pracę N, aby połączyć dwie posortowane tablice.

Scalanie sortowanych tablic

Aby scalić dwie posortowane tablice A[1,5] i B[3,4] wystarczy iterację obu począwszy od początku, wybierając najniższy element pomiędzy dwiema tablicami i zwiększając wskaźnik dla tej tablicy. Skończysz, gdy oba wskaźniki dotrą do końca swoich tablic.

[1,5] [3,4]  --> []
 ^     ^

[1,5] [3,4]  --> [1]
   ^   ^

[1,5] [3,4]  --> [1,3]
   ^     ^

[1,5] [3,4]  --> [1,3,4]
   ^      x

[1,5] [3,4]  --> [1,3,4,5]
    x     x

Runtime = O(A + B)

Merge Sortuj ilustrację

Twój rekurencyjny stos wywołań będzie wyglądał tak. Praca zaczyna się od węzłów dolnych liści i pęcherzyków w górę.

beginning with [1,5,3,4], N = 4, depth k = log(4) = 2

  [1,5]    [3,4]     depth = k-1 (2^1 nodes) * (N/2^1 values to merge per node) == N
[1]  [5]  [3]  [4]   depth = k   (2^2 nodes) * (N/2^2 values to merge per node) == N

Tak więc wykonujesz N pracę na każdym z k poziomów w drzewie, gdzie k = log(N)

N * k = N * log(N)