Jak naprawić nakładanie się okręgu i prostokąta w odpowiedzi na kolizję?
Ponieważ w cyfrowym świecie prawdziwa kolizja prawie nigdy nie ma miejsca, zawsze będziemy mieli sytuację, w której "kolizja" okrąg pokrywa się z prostokątem.
Jak przywrócić okrąg w sytuacji, gdy idealnie zderza się z prostokątem bez nakładania?
Załóżmy, że prostokąt jest zatrzymany (prędkość zerowa) i wyrównany do osi.
Rozwiązałbym ten problem za posteriori podejściem (w dwóch wymiarach).
W skrócie I trzeba rozwiązać to równanie dla t :
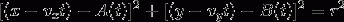
Gdzie:
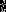 Jest liczbą, która odpowiada na pytanie: ile klatek temu
kolizja zdarzyła się idealnie?
Jest liczbą, która odpowiada na pytanie: ile klatek temu
kolizja zdarzyła się idealnie? Jest promieniem okręgu.
Jest promieniem okręgu.-
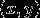 Jest środkiem okręgu
Jest środkiem okręgu 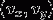 To jego prędkość.
To jego prędkość.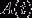 And
And 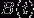 are functions that return the X and y coordinates of
punkt, w którym koło i zderzenie prostokąt (gdy okrąg jest
w pozycji
are functions that return the X and y coordinates of
punkt, w którym koło i zderzenie prostokąt (gdy okrąg jest
w pozycji 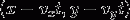 , czyli w pozycji, w której idealnie zderzają się z prostokątem).
, czyli w pozycji, w której idealnie zderzają się z prostokątem).
Ostatnio rozwiązałem podobny problem dla kolizji między kręgami, ale teraz nie znam prawa funkcji a I B.
3 answers
Po latach patrzenia na ten problem i nigdy nie wymyślania idealnego rozwiązania, w końcu to zrobiłem!
To w zasadzie prosty algorytm, bez potrzeby pętli i aproksymacji.
Tak to działa na wyższym poziomie:
- Oblicz czasy przecięcia z płaszczyzną każdej strony, jeśli droga z obecnego punktu do przyszłego punktu przecina tę płaszczyznę.
- Sprawdź kwadrant każdej strony pod kątem przecięcia jednostronnego, zwróć skrzyżowanie.
- określ kąt, z którym kolizja się okrąg.
- Rozwiąż trójkąt między aktualnym punktem, narożnikiem i przecinającym się środkiem (promień od narożnika).
- Oblicz czas, normę i środek przecięcia.
A teraz krwawe szczegóły!
Wejście do funkcji to bounds (który ma lewy, górny, prawy, dolny) oraz bieżący punkt (początek) i przyszły punkt (koniec).
Wyjście jest Klasa zwana przecięciem, która ma x, y, czas, nx i ny.
- {x, y} jest środkiem okręgu w czasie przecięcia.
- czas jest wartością od 0 do 1, Gdzie 0 jest na początku i 1 jest na końcu
- {nx, ny} jest normalną, używaną do odzwierciedlania prędkości w celu określenia nowej prędkości okręgu
Zaczynamy od buforowania zmiennych, których często używamy:
float L = bounds.left;
float T = bounds.top;
float R = bounds.right;
float B = bounds.bottom;
float dx = end.x - start.x;
float dy = end.y - start.y;
I obliczanie czasów przecięcia z płaszczyzną każdej strony (jeśli wektor między startem i koniec przejścia nad tą płaszczyzną):
float ltime = Float.MAX_VALUE;
float rtime = Float.MAX_VALUE;
float ttime = Float.MAX_VALUE;
float btime = Float.MAX_VALUE;
if (start.x - radius < L && end.x + radius > L) {
ltime = ((L - radius) - start.x) / dx;
}
if (start.x + radius > R && end.x - radius < R) {
rtime = (start.x - (R + radius)) / -dx;
}
if (start.y - radius < T && end.y + radius > T) {
ttime = ((T - radius) - start.y) / dy;
}
if (start.y + radius > B && end.y - radius < B) {
btime = (start.y - (B + radius)) / -dy;
}
Teraz staramy się sprawdzić, czy jest to wyłącznie boczne skrzyżowanie (a nie narożnik). Jeśli punkt kolizji leży po stronie to zwróć przecięcie:
if (ltime >= 0.0f && ltime <= 1.0f) {
float ly = dy * ltime + start.y;
if (ly >= T && ly <= B) {
return new Intersection( dx * ltime + start.x, ly, ltime, -1, 0 );
}
}
else if (rtime >= 0.0f && rtime <= 1.0f) {
float ry = dy * rtime + start.y;
if (ry >= T && ry <= B) {
return new Intersection( dx * rtime + start.x, ry, rtime, 1, 0 );
}
}
if (ttime >= 0.0f && ttime <= 1.0f) {
float tx = dx * ttime + start.x;
if (tx >= L && tx <= R) {
return new Intersection( tx, dy * ttime + start.y, ttime, 0, -1 );
}
}
else if (btime >= 0.0f && btime <= 1.0f) {
float bx = dx * btime + start.x;
if (bx >= L && bx <= R) {
return new Intersection( bx, dy * btime + start.y, btime, 0, 1 );
}
}
float cornerX = Float.MAX_VALUE;
float cornerY = Float.MAX_VALUE;
if (ltime != Float.MAX_VALUE) {
cornerX = L;
} else if (rtime != Float.MAX_VALUE) {
cornerX = R;
}
if (ttime != Float.MAX_VALUE) {
cornerY = T;
} else if (btime != Float.MAX_VALUE) {
cornerY = B;
}
// Account for the times where we don't pass over a side but we do hit it's corner
if (cornerX != Float.MAX_VALUE && cornerY == Float.MAX_VALUE) {
cornerY = (dy > 0.0f ? B : T);
}
if (cornerY != Float.MAX_VALUE && cornerX == Float.MAX_VALUE) {
cornerX = (dx > 0.0f ? R : L);
}
double inverseRadius = 1.0 / radius;
double lineLength = Math.sqrt( dx * dx + dy * dy );
double cornerdx = cornerX - start.x;
double cornerdy = cornerY - start.y;
double cornerdist = Math.sqrt( cornerdx * cornerdx + cornerdy * cornerdy );
double innerAngle = Math.acos( (cornerdx * dx + cornerdy * dy) / (lineLength * cornerdist) );
double innerAngleSin = Math.sin( innerAngle );
double angle1Sin = innerAngleSin * cornerdist * inverseRadius;
// The angle is too large, there cannot be an intersection
if (Math.abs( angle1Sin ) > 1.0f) {
return null;
}
double angle1 = Math.PI - Math.asin( angle1Sin );
double angle2 = Math.PI - innerAngle - angle1;
double intersectionDistance = radius * Math.sin( angle2 ) / innerAngleSin;
Teraz, gdy rozwiązaliśmy dla wszystkich stron i kątów, możemy określić czas i wszystko inne:
// Solve for time
float time = (float)(intersectionDistance / lineLength);
// If time is outside the boundaries, return null. This algorithm can
// return a negative time which indicates the previous intersection.
if (time > 1.0f || time < 0.0f) {
return null;
}
// Solve the intersection and normal
float ix = time * dx + start.x;
float iy = time * dy + start.y;
float nx = (float)((ix - cornerX) * inverseRadius);
float ny = (float)((iy - cornerY) * inverseRadius);
return new Intersection( ix, iy, time, nx, ny );
Miałem nadzieję, że będzie sposób, aby to zrobić bez funkcji trygonometrycznych, ale musiałem się poddać!
Oto przykład o tym, że nazwałem go i użyłem go do obliczenia nowej pozycji okręgu używając normalnego do odbicia i czasu przecięcia do obliczenia wielkości odbicia:
Intersection inter = handleIntersection( bounds, start, end, radius );
if (inter != null)
{
// Project Future Position
float remainingTime = 1.0f - inter.time;
float dx = end.x - start.x;
float dy = end.y - start.y;
float dot = dx * inter.nx + dy * inter.ny;
float ndx = dx - 2 * dot * inter.nx;
float ndy = dy - 2 * dot * inter.ny;
float newx = inter.x + ndx * remainingTime;
float newy = inter.y + ndy * remainingTime;
// new circle position = {newx, newy}
}
I zamieściłem Pełny kod na pastebin Z całkowicie interaktywnym przykładem, w którym możesz wykreślić punkty początkowe i końcowe i pokazuje czas i wynikowe odbicie od prostokąta.
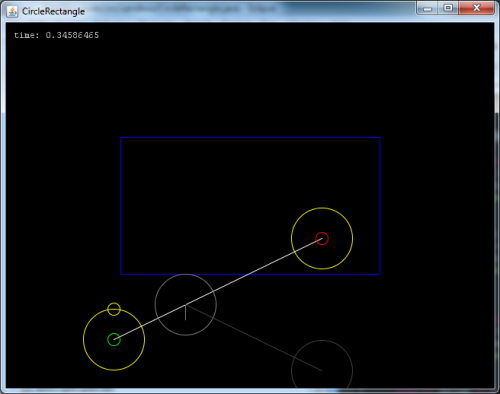
Jeśli chcesz go uruchomić od razu musisz pobrać kod z mojego bloga , w przeciwnym razie wsadź go do własnej aplikacji Java2D.
Edytuj: Zmodyfikowałem kod w pastebinie, aby zawierał również punkt kolizji, a także wprowadziłem kilka ulepszeń prędkości.
Edytuj: Możesz zmodyfikować to dla obracającego się prostokąta, używając kąta tego prostokąta, aby usunąć obrócenie prostokąta z punktami początkowymi i końcowymi okręgu. Wykonasz sprawdzenie przecięcia, a następnie obróć powstałe punkty i normalne.
Edytuj: Zmodyfikowałem kod na pastebin kończy się wcześnie, jeśli objętość obwiedni ścieżki okręgu nie przecina się z prostokątem.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2013-09-15 04:32:56
Znalezienie momentu kontaktu nie jest zbyt trudne:
Potrzebne jest położenie okręgu i prostokąta w punkcie czasowym przed kolizją (B) i punkcie czasowym po (A). Oblicz odległość od środka okręgu do linii prostokąta, z którym koliduje w momentach A i B (tj. wspólny wzór na odległość od punktu do linii), a następnie czas kolizji wynosi:
tC = dt*(dB-R)/(dA+dB),
Gdzie tC to czas kolizji, dt to timestep, dB to odległość do linii przed kolizją dA jest odległością po kolizji, A R promieniem okręgu.
Zakłada to, że wszystko jest lokalnie liniowe, to znaczy, że twój czas jest stosunkowo mały i tak, że prędkość itp. nie zmienia się zbyt wiele w czasie, w którym obliczasz zderzenie. Jest to w końcu punkt timestepów: w tym, że z wystarczająco małym timestepem, nieliniowe problemy są lokalnie liniowe. W powyższym równaniu korzystam z tego: dB-R jest odległością od koła do linii, a dA + dB jest całkowitą odległością przesuniętą, więc to pytanie zrównuje stosunek odległości do stosunku czasu zakładając, że wszystko jest w przybliżeniu liniowe w czasie. (Oczywiście, w momencie zderzenia przybliżenie liniowe nie jest najlepsze, ale aby znaleźć moment zderzenia, pytanie brzmi, czy jest liniowe w przedziale czasowym do do momentu zderzenia.)
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2013-09-10 14:30:57
To problem nieliniowy, prawda?
Wykonujesz krok czasowy i przesuwasz piłkę po jej przemieszczeniu obliczonym na podstawie prędkości na początku kroku. Jeśli zauważysz nakładanie się, Zmniejsz rozmiar kroku i Przelicz ponownie zbieżność.
Czy zakładasz, że kulki i prostokąty są sztywne, bez deformacji? Bezproblemowy kontakt? Jak poradzisz sobie z ruchem piłki po nawiązaniu kontaktu? Czy zmieniasz układ współrzędnych styku (normalny + tangencjalne), obliczanie, a następnie przekształcanie z powrotem?
To nie jest trywialny problem.
Może powinieneś przyjrzeć się silnikowi fizyki, jak Box2D , zamiast samemu go kodować.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2013-09-09 19:34:39