Algorytm drzewa sufiksowego ukkonena w prostym języku angielskim
Czuję się trochę gruba w tym momencie. Spędziłem wiele dni próbując w pełni owinąć głowę wokół konstrukcji drzewa sufiksów, ale ponieważ nie mam matematycznego tła, wiele wyjaśnień mi umyka, ponieważ zaczynają nadmiernie używać symboli matematycznych. Najbliżej dobrego wyjaśnienia, które znalazłem, jest Szybkie wyszukiwanie ciągów za pomocą drzew Przyrostkowych, ale on glossy na różnych punktach i niektóre aspekty algorytmu pozostają niejasne.
A krok po kroku wyjaśnienie tego algorytmu tutaj na Stack Overflow byłoby nieocenione dla wielu innych oprócz mnie, jestem pewien.
Dla odniesienia, oto artykuł Ukkonena na temat algorytmu: http://www.cs.helsinki.fi/u/ukkonen/SuffixT1withFigs.pdf
Moje podstawowe zrozumienie, jak na razie:
- I need to iterate through each prefix P of a dan string T
- muszę iterować przez każdy sufiks S W prefiksie P i dodać to do drzewa
- aby dodać sufiks S do drzewo, muszę iterować przez każdy znak w S, z iteracjami składającymi się albo z przechodzenia w dół istniejącej gałęzi, która zaczyna się od tego samego zestawu znaków C W S i potencjalnie dzielenie krawędzi na potomnych węzłów, gdy osiągnę różny znak w sufiksie, lub jeśli nie było pasującej krawędzi, aby przejść w dół. Gdy nie znaleziono pasującej krawędzi dla C, tworzona jest nowa krawędź liścia dla C.
Podstawowym algorytmem wydaje się być O (n2), Jak jest wskazywany w większości wyjaśnień, ponieważ musimy przejść przez wszystkie prefiksy, a następnie musimy przejść przez każdy z sufiksów dla każdego prefiksu. Algorytm ukkonena jest najwyraźniej unikalny ze względu na technikę wskaźnika sufiksu, której używa, chociaż myślę, że to jest tym, co mam problem ze zrozumieniem.
Ja też mam problemy ze zrozumieniem:- dokładnie kiedy i jak "aktywny punkt" jest przypisany, używany i zmieniany
- co się dzieje z kanonizacyjny aspekt algorytmu
- dlaczego implementacje, które widziałem, muszą "naprawić" zmienne obwiedniowe, których używają
Oto kompletny C # kod źródłowy. Nie tylko działa poprawnie, ale obsługuje automatyczną kanonizację i renderuje ładniej wyglądający Wykres tekstowy na wyjściu. Kod źródłowy i Przykładowe wyjście znajduje się w:
Aktualizacja 2017-11-04
Po wielu latach Znalazłem nowe zastosowanie dla drzew sufiksów i zaimplementowałem algorytm w JavaScript . Gist jest poniżej. Powinno być wolne od błędów. Zrzut go do pliku js, npm install chalk z tej samej lokalizacji, a następnie uruchom z node.js, aby zobaczyć jakieś kolorowe wyjście. Istnieje rozebrana wersja w tym samym Gist, bez żadnego kodu debugowania.
Https://gist.github.com/axefrog/c347bf0f5e0723cbd09b1aaed6ec6fc6
7 answers
Poniżej przedstawiono próbę opisania algorytmu Ukkonena, najpierw pokazując, co robi, gdy ciąg znaków jest prosty (tzn. nie zawiera żadnych powtarzających się znaków), a następnie rozszerzając go do pełnego algorytmu.
Najpierw kilka wstępnych oświadczeń.
-
To, co budujemy, jest W zasadzie jak poszukiwania. Więc tam jest węzłem głównym, wychodzące z niego krawędzie prowadzące do nowych węzłów, a kolejne krawędzie wychodzące z nich i tak dalej
Ale: W przeciwieństwie do wyszukiwania trie, etykiety krawędzi nie są pojedyncze postaci. Zamiast tego każda krawędź jest oznaczana za pomocą pary liczb całkowitych
[from,to]. Są to wskaźniki do tekstu. W tym sensie każdy edge posiada etykietę łańcuchową o dowolnej długości, ale zajmuje tylko O (1) spacja (Dwa wskaźniki).
Podstawowa zasada
Chciałbym najpierw zademonstrować jak stworzyć drzewo sufiksów szczególnie prosty ciąg, ciąg bez powtarzających się znaków:
abc
Algorytm działa w krokach, od lewej do prawej. Istnieje jeden krok dla każdego znaku ciągu . Każdy krok może obejmować więcej niż jedną indywidualną operację, ale zobaczymy (patrz końcowe obserwacje na końcu), że całkowita liczba operacji wynosi O (n).
Więc zaczynamy od W lewo i najpierw wstawiamy tylko pojedynczy znak
a tworząc krawędź z węzła głównego (na lewy) do liścia,
i oznaczanie go jako [0,#], co oznacza, że krawędź reprezentuje
substring zaczynający się na pozycji 0 i kończący się na bieżący koniec. I
użyj symbolu #, aby oznaczać bieżący koniec, który znajduje się na pozycji 1
(zaraz po a).
Mamy więc drzewo inicjalne, które wygląda tak:

A to oznacza:

Teraz przechodzimy do pozycji 2 (zaraz po b). nasz cel na każdym kroku
jest wstawianie wszystkich sufiksów do bieżącej pozycji . Robimy to
by
- rozszerzenie istniejącego
a-edge doab - wstawianie jednej nowej krawędzi dla
b
W naszej reprezentacji wygląda to tak
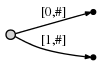
A to oznacza:

Obserwujemy dwie rzeczy:
- reprezentacja krawędzi dla
abjest tym samym jak to było kiedyś w drzewie początkowym:[0,#]. Jego znaczenie zmieniło się automatycznie ponieważ zaktualizowaliśmy obecną pozycję#z 1 do 2. - Każda krawędź pochłania o (1) przestrzeń, ponieważ składa się tylko z dwóch wskaĺşniki do tekstu, bez wzglÄ ™ du na to, ile znakĂłw reprezentuje.
Następnie ponownie zwiększamy pozycję i aktualizujemy drzewo dodając
a c do każdej istniejącej krawędzi i wstawianie jednej nowej krawędzi dla nowej
przyrostek c.
W naszym reprezentacja wygląda tak

A to oznacza:

Obserwujemy:
- drzewo jest poprawnym drzewem sufiksu do aktualnej pozycji po każdym kroku
- jest tyle kroków, ile znaków w tekście
- Ilość pracy w każdym kroku wynosi O(1), ponieważ wszystkie istniejące krawędzie
są aktualizowane automatycznie przez inkrementację
#i wstawianie jeden nową krawędź dla znaku końcowego można wykonać w O (1) czas. Dlatego dla Ciągu o długości n wymagany jest tylko Czas O (n).
Pierwsze rozszerzenie: proste powtórzenia
Oczywiście to działa tak ładnie tylko dlatego, że nasz ciąg nie zawierają wszelkie powtórzenia. Teraz przyjrzymy się bardziej realistycznemu ciągowi:
abcabxabcd
Zaczyna się od abc jak w poprzednim przykładzie, następnie ab jest powtarzane
a po nim x, a następnie abc powtarza się d.
Kroki od 1 do 3: po pierwszych 3 krokach mamy drzewo z poprzedniego przykładu:

Krok 4: przenosimy # na pozycję 4. To niejawnie aktualizuje wszystkie istniejące
krawędzie do tego:

I musimy wstawić końcowy przyrostek bieżącego kroku, a, w
korzeń.
Zanim to zrobimy, Wprowadzamy jeszcze dwie zmienne (oprócz
#), który z oczywiście byliśmy tam cały czas, ale nie wykorzystaliśmy
do tej pory:
- aktywny punkt, który jest potrójnym
(active_node,active_edge,active_length) -
remainder, która jest liczbą całkowitą wskazującą ile nowych przyrostków musimy wstawić
Dokładne znaczenie tych dwóch wyjaśni się wkrótce, ale na razie powiedzmy:
- w prostym przykładzie
abcpunkt aktywny był zawsze(root,'\0x',0), tzn.active_nodebył węzłem głównym,active_edgezostał określony jako znak null'\0x'iactive_lengthwynosił zero. Efektem tego było to, że jedna nowa krawędź, która wstawiamy w każdym kroku wstawiamy do węzła głównego jako świeżo stworzona krawędź. Wkrótce zobaczymy, dlaczego potrójna jest konieczna do reprezentuj te informacje. -
remainderbył zawsze ustawiony na 1 na początku każdego krok. Znaczenie tego było takie, że liczba przyrostków, które musieliśmy aktywnie wstawić na końcu każdego kroku było 1 (zawsze tylko finał charakter).
a w korzeniu, zauważamy, że istnieje już wychodzący
krawędź zaczynająca się od a, a konkretnie: abca. Oto co robimy w
taki przypadek:
- My nie wstawiamy świeżą krawędź
[4,#]do węzła głównego. Zamiast tego My wystarczy zauważyć, że przyrostekajest już w naszym drzewo. Kończy się w środku dłuższej krawędzi, ale nie jesteśmy / align = "left" / My tylko zostaw wszystko tak, jak jest. - ustawiamy punkt aktywny na
(root,'a',1). Oznacza to, że aktywne punkt znajduje się teraz gdzieś w środku wychodzącej krawędzi węzła głównego, która zaczyna się oda, konkretnie po pozycji 1 na tej krawędzi. My zauważ, że krawędź jest określona po prostu przez jej pierwszy znaka. To wystarczy, ponieważ może być tylko jedna krawędź zaczynając od dowolnego konkretnego znaku (potwierdź, że jest to prawda po przeczytaniu całej opis). - zwiększamy również
remainder, więc na początku następnego kroku będzie 2.
Obserwacja: gdy końcowy sufiks, który musimy wstawić znajduje się
istnieje w drzewie już , samo drzewo jest nie zmienione w ogóle (aktualizujemy tylko aktywny punkt i remainder). Drzewo
nie jest więc dokładną reprezentacją drzewa sufiksów aż do
aktualna pozycja więcej, ale zawiera wszystkie przyrostki (ponieważ końcowy
sufiks a zawiera w domyśle ). Stąd, oprócz aktualizacji
zmiennych (które są wszystkie o stałej długości, więc jest to O (1)), było
żadna praca nie została wykonana w tym kroku.
Krok 5: aktualizujemy aktualną pozycję # do 5. To
w ten sposób drzewo jest automatycznie aktualizowane do tego:

I ponieważ remainder jest 2, musimy wstawić dwa końcowe
przyrostki aktualnej pozycji: ab i b. Jest to w zasadzie dlatego, że:
- przyrostek
az poprzedniego kroku nigdy nie był prawidłowy / align = "left" / Tak więc pozostało , a ponieważ rozwinęliśmy jedną krok, teraz wzrosła zadoab. - i musimy wstawić nową krawędź
b.
W praktyce oznacza to, że idziemy do punktu aktywnego (który wskazuje na
za {[3] } na tym, co jest teraz abcab krawędzią), i wstawić
aktualny znak końcowy b. ale: znowu okazuje się, że b jest
również już obecne na tej samej krawędzi.
- zaktualizuj aktywny punkt do
(root,'a',2)(ten sam węzeł i krawędź jak wcześniej, ale teraz wskazujemy zab) - zwiększ
remainderdo 3, ponieważ nadal nie mamy prawidłowo wstawiamy ostatnią krawędź z poprzedniego kroku i nie wstawiamy aktualna krawędź końcowa.
Żeby było jasne: mieliśmy aby wstawić ab i b w bieżącym kroku, ale
ponieważ ab został już znaleziony, zaktualizowaliśmy aktywny punkt i zrobiliśmy
nawet nie próbować wstawić b. Dlaczego? Bo jeśli {[9] } jest na drzewie,
każdy przyrostek tego (łącznie z b) musi znajdować się w drzewie,
też. Być może tylko w domyśle , ale musi tam być, ponieważ
sposób, w jaki do tej pory zbudowaliśmy drzewo.
Przechodzimy do kroku 6 zwiększając #. Drzewo jest
automatycznie aktualizowane do:

Ponieważ remainder is 3 , musimy wstawić abx, bx oraz
x. Punkt aktywny mówi nam, gdzie ab się kończy, więc musimy tylko
Skocz tam i włóż x. Rzeczywiście, x Jeszcze nie ma, więc my
podziel krawędź abcabx i wstaw wewnętrzny węzeł:

Reprezentacje krawędzi są nadal wskaźnikami do tekstu, więc rozdzielenie i wstawianie wewnętrznego węzła można wykonać w czasie O(1).
Więc my zajmowali się abx i decrement remainder do 2. Teraz my
należy wstawić następny przyrostek, bx. Ale zanim to zrobimy
musimy zaktualizować aktywny punkt. Zasady tego, po podzieleniu
i wstawianie krawędzi, będzie wywoływane reguła 1 poniżej, i ma ona zastosowanie, gdy
active_node jest root (poznamy regułę 3 dla innych przypadków dalej
poniżej). Oto zasada 1:
Po wstawieniu z roota,
active_nodepozostaje korzeniemactive_edgejest ustawione na pierwszy znak nowego sufiksu we trzeba wstawić, czylibactive_lengthzmniejsza się o 1
Stąd nowy potrójny punkt aktywny (root,'b',1) wskazuje, że
Następna wstawka musi być wykonana na krawędzi bcabx, za 1 znakiem,
tj. za b. Możemy zidentyfikować punkt wstawiania w czasie O(1) i
sprawdź, czy x jest już obecny, czy nie. Jeśli był obecny, my
zakończyłoby obecny krok i zostawiłoby wszystko tak, jak to jest. Ale x
nie występuje, więc wstawiamy go dzieląc krawędź:

Ponownie, zajęło to O(1) czasu i aktualizujemy remainder do 1 i
punkt aktywny do (root,'x',0), jak stwierdza zasada 1.
Jeśli podzielimy krawędź i wstawimy nowy węzeł, a jeśli to jest Nie pierwszy węzeł utworzony podczas bieżącego kroku, łączymy poprzednio wstawiony węzeł i nowy węzeł poprzez specjalny wskaźnik, przyrostek link . Zobaczymy później, dlaczego jest to przydatne. Oto, co otrzymujemy, link przyrostkowy jest reprezentowany jako kropkowana krawędź:

Nadal musimy wstawić końcowy przyrostek bieżącego kroku,
x. Ponieważ składowa active_length aktywnego węzła spadła
do 0, ostateczna wkładka jest wykonywana bezpośrednio u nasady. Ponieważ nie ma
wychodząca krawędź w węźle głównym zaczynającym się od x, wstawiamy nowe
edge:

Jak widać, w bieżącym kroku wykonano wszystkie pozostałe wstawki.
Przechodzimy do Krok 7 ustawiając #=7, który automatycznie dopisze następny znak,
a, do wszystkich krawędzi liści, jak zawsze. Następnie staramy się wstawić nowy finał
znak do punktu aktywnego (korzenia) i stwierdzają, że jest tam
już. Więc kończymy bieżący krok bez wkładania czegokolwiek i
zaktualizuj aktywny punkt do (root,'a',1).
W krok 8, #=8, dołączamy b, i jak widać wcześniej, to tylko
oznacza, że aktualizujemy aktywny punkt do (root,'a',2) i zwiększamy remainder bez wykonywania
cokolwiek innego, ponieważ b jest już obecny. jednak zauważamy (w czasie O(1)), że punkt aktywny
jest teraz na końcu krawędzi. Odzwierciedlamy to poprzez ponowne ustawienie go do
(node1,'\0x',0). Tutaj używam node1, aby odnieść się do
węzeł wewnętrzny krawędź ab kończy się na.
Następnie, w kroku #=9, musimy wstawić "c" a to pomoże nam
zrozumieć ostateczną sztuczkę:
Second extension: Using sufiks links
Jak zawsze, aktualizacja # dołącza c automatycznie do krawędzi liścia
i idziemy do aktywnego punktu, aby zobaczyć, czy możemy wstawić "c". Odwraca się
z "c" istnieje już na tej krawędzi, więc ustawiamy punkt aktywny na
(node1,'c',1), increment remainder i nic więcej nie robić.
Teraz w kroku #=10, remainder jest 4, więc najpierw musimy wstawić
abcd (który pozostaje od 3 kroków temu) przez wstawienie d na aktywne
punkt.
Próba Wstawienia d w punkcie aktywnym powoduje podział krawędzi w
O (1) czas:

active_node, z którego zainicjowano podział, oznaczono w
czerwony powyżej. Oto ostateczna reguła reguła 3:
Po oddzieleniu krawędzi od
active_node, która nie jest korzeniem węzeł, podążamy za łączem sufiksowym wychodzącym z tego węzła, jeśli jest dowolne, i zresetowaćactive_nodedo węzeł, na który wskazuje. Jeśli jest brak łącza przyrostkowego, ustawiamyactive_nodena root.active_edgeiactive_lengthpozostają bez zmian.
Więc punkt aktywny jest teraz (node2,'c',1), A node2 jest zaznaczony w
czerwony poniżej:

Ponieważ wstawianie abcd jest kompletne, zmniejszamy remainder do
3 i rozważmy następny pozostały przyrostek bieżącego kroku,
bcd. Reguła 3 ustawiła aktywny punkt tylko na prawy węzeł i krawędź
więc wstawianie bcd może być wykonane przez wystarczy wstawić jego ostateczny znak
d w punkcie aktywnym.
To powoduje kolejny podział krawędzi, i z powodu Zasady 2 , mamy musi utworzyć łącze przyrostkowe z wcześniej wstawionego węzła do nowego jeden:

Obserwujemy: łącza przyrostkowe pozwalają nam zresetować aktywny punkt, więc
moĹźe wykonaÄ ‡ nastÄ ™ pny pozostaĹ 'y insert przy wysiĹ' ku O(1). Zobacz też
wykres powyżej, aby potwierdzić, że węzeł indeed at label ab jest połączony na
węzeł w b (jego sufiks), a węzeł w abc jest połączony z
bc.
Bieżący krok nie został jeszcze zakończony. remainder jest teraz 2, a my
należy postępować zgodnie z zasadą 3, aby ponownie zresetować aktywny punkt. Ponieważ
current active_node (czerwony powyżej) nie ma łącza przyrostkowego, resetujemy do
root. Punktem aktywnym jest teraz (root,'c',1).
Stąd Następna wstawka występuje na jednej wychodzącej krawędzi węzła głównego
którego etykieta zaczyna się od c: cabxabcd, za pierwszą postacią,
tj. za c. Powoduje to kolejny podział:

A ponieważ wiąże się to z utworzeniem nowego węzła wewnętrznego, podążamy za reguła 2 i ustawić nowy łącze przyrostkowe z wcześniej utworzonego wewnętrznego węzeł:

(używam Graphviz Dot dla tych małych wykresy. Nowy sufiks link spowodował, że kropka ponownie uporządkowała istniejący krawędziach, więc sprawdź uważnie, aby potwierdzić, że jedyną rzeczą, która była wstawiony powyżej jest nowy przyrostek link.)
Z to, remainder można ustawić na 1, A ponieważ active_node jest
root, używamy zasady 1, aby zaktualizować aktywny punkt do (root,'d',0). To
oznacza, że ostatnią wstawką bieżącego kroku jest wstawienie pojedynczego d
w korzeniu:

W każdym kroku przesuwamy
#do przodu o 1 pozycję. To automatycznie aktualizuje wszystkie węzły liścia w O (1) czas.Ale nie dotyczy to a) żadnych przyrostków pozostałych z poprzedniego kroki, oraz b) z jednym końcowym znakiem bieżącego kroku.
remaindermówi nam, ile dodatkowych wkładek potrzebujemy do make. Wstawki te odpowiadają pojedynczo ostatnim przyrostkom łańcuch kończący się na bieżącej pozycji#. Rozważamy jeden po drugiej i zrobić wkładkę. ważne: każda wkładka jest zrobione w O (1) czasie od aktywny punkt podpowiada nam dokładnie, gdzie go, i musimy dodać tylko jeden znak w aktywnym punkt. Dlaczego? Ponieważ pozostałe znaki są zawarte niejawnie (w przeciwnym razie aktywny punkt nie byłby tam, gdzie jest).Po każdej takiej wstawce dekretujemy
remainderi podążamy za łącznik przyrostkowy, jeśli istnieje. Jeśli nie, przechodzimy do roota(reguła 3). Jeśli my są już w korzeniu, modyfikujemy aktywny punkt za pomocą reguły 1. W w każdym przypadku wystarczy tylko O (1) czas.Jeśli podczas jednej z tych wstawek okaże się, że postać, którą chcemy do wstawienia jest już, nic nie robimy i kończymy bieżący krok, nawet jeśli
remainder>0. Powodem jest to, że każdy wstawki, które pozostaną, będą przyrostkami tego, który właśnie próbowaliśmy make. Stąd wszystkie one są niejawne w bieżącym drzewie. Fakt żeremainder> 0 sprawia, że mamy do czynienia z pozostałymi przyrostkami później.Co jeśli na końcu algorytmu
remainder>0? To będzie wielkość liter, gdy koniec tekstu jest podłańcuchem, który wystąpił gdzieś wcześniej. W takim przypadku musimy dodać jeden dodatkowy znak na końcu łańcucha, który wcześniej nie wystąpił. W Literatura, Zwykle znak dolara$jest używany jako symbol dla to. jakie to ma znaczenie? -- > jeśli później użyjemy ukończonego drzewa sufiksów do wyszukiwania sufiksów, musimy zaakceptować dopasowania tylko wtedy, gdy kończą się liściem . W przeciwnym razie dostalibyśmy dużo fałszywe dopasowania, ponieważ istnieje wiele ciągów w domyśle zawartych w drzewie, które nie są rzeczywistymi sufiksami głównego ciągu. Wymuszanieremainder, aby na końcu było 0 jest zasadniczo sposobem zapewnienia, że wszystkie sufiksy kończą się na węźle liścia. jednakże, jeśli chcemy użyć drzewa do wyszukiwania ogólnych podłańcuchów , a nie tylko sufiksów głównego ciągu, Ten ostatni krok nie jest wymagany, jak sugeruje komentarz OP poniżej.Jaka jest więc złożoność całego algorytmu? Jeśli tekst jest n znaków długości, oczywiście jest n kroków (lub n+1 jeśli dodamy znak dolara). Na każdym kroku albo nic nie robimy (poza aktualizowanie zmiennych), lub wykonujemy
remainderwstawki, każdy biorąc O (1) czas. Ponieważremainderwskazuje, ile razy nic nie zrobiliśmy w poprzednich krokach i jest malejąca dla każdej wkładki, którą wykonujemy teraz, całkowita liczba razy robimy coś jest dokładnie n (lub n+1). Stąd całkowita złożoność to O (n).-
Jest jednak jedna mała rzecz, której właściwie nie wyjaśniłem: Może się zdarzyć, że podążamy za linkiem sufiksowym, aktualizujemy aktywne wskazywać, a następnie stwierdzić, że jego
active_lengthskładowa nie pracuj dobrze z nowymactive_node. Na przykład rozważmy sytuację w ten sposób:

(przerywane linie wskazują resztę drzewa. Linia przerywana jest łącznik przyrostkowy.)
Teraz niech active point be (red,'d',3), więc wskazuje na miejsce
za f na defg krawędzi. Teraz Załóżmy, że zrobiliśmy niezbędne
aktualizacje, a teraz postępuj zgodnie z łączem przyrostka, aby zaktualizować aktywny punkt
zgodnie z zasadą 3. Nowy aktywny punkt to (green,'d',3). Jednakże,
d-krawędź wychodząca z zielonego węzła to de, więc ma tylko 2
postaci. Aby znaleźć właściwy punkt aktywny, oczywiście
należy podążać za tą krawędzią do niebieskiego węzła i zresetować do (blue,'f',1).
W szczególnie złym przypadku, active_length może być tak duża jak
remainder, która może być tak duża jak N. i może się zdarzyć
że aby znaleźć właściwy punkt aktywny, musimy nie tylko przeskoczyć nad jednym
węzeł wewnętrzny, ale być może wiele, aż do n w najgorszym przypadku. Czy to
oznacza, że algorytm ma ukryte O (n2) złożoność, ponieważ
w każdym kroku remainder jest na ogół O (n) , A po korekcie
do aktywnego węzła po zastosowaniu łącza przyrostkowego może być również O (n)?
Nie. Powodem jest to, że jeśli rzeczywiście musimy dostosować aktywny punkt
(np. z zielonego na niebieski jak wyżej), co prowadzi nas do nowego węzła, który
posiada własne łącze przyrostkowe, a active_length zostanie zredukowane. Jako
podążamy w dół łańcucha łączników sufiksowych wykonujemy Pozostałe wkładki, active_length można tylko
zmniejszenie, a ilość korekt active-point możemy dokonać na
droga nie może być większa niż active_length w danym momencie. Od
active_length nigdy nie może być większy niż remainder i remainder
jest O (n) nie tylko w każdym kroku, ale całkowita suma przyrosty
[26]} w trakcie całego procesu jest
O (n) również liczba korekt punktu aktywnego jest ograniczona przez
O (n).
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-11-08 19:49:17
Próbowałem zaimplementować drzewo sufiksów z podejściem podanym w odpowiedzi jogojapana, ale nie zadziałało w niektórych przypadkach ze względu na sformułowania używane do zasad. Co więcej, wspomniałem, że nikt nie zdołał zaimplementować absolutnie poprawnego drzewa sufiksów przy użyciu tego podejścia. Poniżej napiszę "Przegląd" odpowiedzi jogojapana z pewnymi modyfikacjami do Regulaminu. Opiszę również przypadek, gdy zapomnimy stworzyć Ważne przyrostek linki.
Użyte dodatkowe zmienne
- active point - potrójny (active_node; active_edge; active_length), pokazujący, skąd musimy zacząć wstawiać nowy sufiks.
- Rest - pokazuje liczbę przyrostków, które musimy dodać jawnie. Na przykład, jeśli nasze słowo to 'abcaabca', a rest = 3, oznacza to, że musimy przetworzyć 3 ostatnie przyrostki: bca, ca i a .
Użyjmy pojęcie węzła wewnętrznego - wszystkie węzły, z wyjątkiem korzenia i liści są węzłami wewnętrznymi.
Obserwacja 1
Gdy końcowy sufiks, który musimy wstawić, okaże się już istniał w drzewie, samo drzewo w ogóle nie jest zmieniane (aktualizujemy tylko active point i remainder).
Obserwacja 2
Jeśli w pewnym punkcie active_length jest większa lub równa długości bieżącej krawędzi (edge_length), przesuwamy naszą active point w dół, aż edge_length jest ściśle większa niż active_length.
Reguła 1
Jeśli po wstawieniu z aktywnego węzła = root , długość aktywna jest większa od 0, wtedy:
- aktywny węzeł nie ulega zmianie
- długość aktywna jest zmniejszona
- aktywna krawędź jest przesunięta w prawo (do pierwszego znaku następnego sufiks musimy wstawić)
Reguła 2
Jeśli utworzymy nowy wewnętrzny węzeł lub zrobić inserter z wewnętrznego węzła , a to nie jest pierwszy taki wewnętrzny węzeł w bieżącym kroku, następnie łączymy poprzedni taki węzeł z tym jednym poprzez łącze przyrostkowe.
Ta definicja Rule 2 różni się od jogojapan', ponieważ tutaj bierzemy pod uwagę nie tylko nowo utworzone węzły wewnętrzne, ale także węzły wewnętrzne, z których wykonujemy wstawianie.
Reguła 3
Po wstawieniu z aktywnego węzła , który nie jest węzłem root , musimy podążać za łączem przyrostkowym i ustawić aktywny węzeł na węzeł, do którego wskazuje. Jeśli nie ma łącza przyrostkowego, Ustaw aktywny węzeł na root węzeł. Tak czy inaczej, active edge i długość aktywna pozostaje bez zmian.
W tej definicji Rule 3 rozważamy również wstawki węzłów liściowych (nie tylko węzłów dzielonych).
I wreszcie obserwacja 3:
Gdy symbol, który chcemy dodać do drzewa, jest już na krawędzi, zgodnie z Observation 1, aktualizujemy tylko active point i remainder, pozostawiając drzewo bez zmian. Ale jeśli istnieje wewnętrzny węzeł oznaczony jako z sufiksem link , musimy połączyć ten węzeł z naszym bieżącym active node poprzez łącze przyrostkowe.
Spójrzmy na przykład drzewa sufiksów dla cdddcdc jeśli dodamy łącze sufiksowe w takim przypadku, a jeśli nie:
-
Jeśli Nie połączymy węzły poprzez łącze przyrostkowe:
- przed dodaniem ostatniej litery c :

- Po dodaniu ostatniej litery c :

-
Jeśli do połącz węzły za pomocą łącza przyrostkowego:
- przed dodaniem ostatniej litery c :

- Po dodaniu ostatniej litery c :

Wydaje się, że nie ma znaczącej różnicy: w drugim przypadku są jeszcze dwa łącza przyrostkowe. Ale te łącza przyrostkowe są poprawne , a jeden z nich-od niebieskiego węzła do Czerwonego-jest bardzo Ważne dla naszego podejścia z aktywnym punktem. Problem polega na tym, że jeśli nie umieścimy tutaj łącza przyrostkowego, później, gdy dodamy nowe litery do drzewa, możemy pominąć dodawanie niektórych węzłów do drzewa ze względu na Rule 3, ponieważ zgodnie z nim, jeśli nie ma łącza przyrostkowego, to musimy umieścić active_node do korzenia.
Kiedy dodaliśmy ostatnią literę do drzewa, czerwony węzeł miał już istniał zanim zrobiliśmy wstawkę z niebieskiego węzła (krawędź labled " c " ). Ponieważ w niebieskim węźle pojawiła się wstawka, oznaczamy ją jako potrzebującą łącza przyrostkowego. Następnie, opierając się na podejściu active point, active node został ustawiony na czerwony węzeł. Ale nie robimy wstawki z czerwonego węzła, ponieważ litera ' c ' jest już na krawędzi. Czy to znaczy, że niebieski węzeł musi być pozostawiony bez łącza przyrostkowego? Nie, musimy połączyć niebieski węzeł z Czerwonym poprzez łącze przyrostkowe. Dlaczego to jest poprawne? Ponieważ aktywny podejście punktowe gwarantuje, że dotrzemy we właściwe miejsce, tj. do następnego miejsca, gdzie musimy przetworzyć wstawkę krótszą.
Mam nadzieję, że ten "przegląd" w połączeniu ze szczegółową odpowiedzią jogojapana pomoże komuś zaimplementować własne drzewo sufiksów.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2016-10-10 23:15:27
Przepraszam, jeśli moja odpowiedź wydaje się zbędna, ale zaimplementowałem algorytm Ukkonena niedawno i zmagałem się z nim przez wiele dni; musiałem przeczytać wiele artykułów na ten temat, aby zrozumieć dlaczego i jak niektórych podstawowych aspektów algorytmu.
Uznałem podejście "reguł" poprzednich odpowiedzi za nieprzydatne do zrozumienia podstawowych powodów , więc napisałem wszystko poniżej koncentrując się wyłącznie na pragmatyce. Jeśli zmagałeś się z innymi wyjaśnienia, tak jak ja, być może moje uzupełniające Wyjaśnienie sprawi, że "klik" dla Ciebie.
Swoją implementację C# opublikowałem tutaj: https://github.com/baratgabor/SuffixTree
proszę zauważyć, że nie jestem ekspertem w tym temacie, więc poniższe sekcje mogą zawierać nieścisłości (lub co gorsza). Jeśli napotkasz jakieś, możesz je edytować.
Wymagania wstępne
Punkt wyjścia poniższego wyjaśnienia zakłada, że jesteś zaznajomiony z zawartość i wykorzystanie drzew przyrostków oraz charakterystyka algorytmu Ukkonena, np. jak rozszerzasz drzewo przyrostków znak po znaku, Od początku do końca. Zakładam, że przeczytałeś już inne wyjaśnienia.
(jednak musiałem dodać trochę podstawowej narracji dla flow, więc początek może rzeczywiście wydawać się zbędny.)
Najciekawszą częścią jest wyjaśnienie różnicy między używaniem linków przyrostkowych a ponownym skanowaniem z root . To właśnie przyprawiło mnie o wiele błędów i bólów głowy w mojej implementacji.
Otwarte węzły liściowe i ich ograniczenia
Jestem pewien, że już wiesz, że najbardziej podstawową 'sztuczką' jest uświadomienie sobie, że możemy po prostu pozostawić koniec sufiksów 'open', tzn. odnosić się do bieżącej długości łańcucha zamiast ustawiać koniec na wartość statyczną. W ten sposób, gdy dodamy dodatkowe znaki, znaki te będą domyślnie dodawane do wszystkich etykiet sufiksów, bez konieczności odwiedź i zaktualizuj wszystkie z nich.
Ale to otwarte zakończenie sufiksów – z oczywistych powodów-działa tylko dla węzłów, które reprezentują koniec łańcucha, tj. węzły liściowe w strukturze drzewa. Operacje rozgałęzienia, które wykonujemy na drzewie (dodawanie nowych węzłów gałęzi i węzłów liści) nie będą się automatycznie rozprzestrzeniać wszędzie tam, gdzie trzeba.
jest to prawdopodobnie elementarne i nie wymagałoby wzmianki, że powtarzające się podciągi nie pojawiają się wyraźnie w drzewie, ponieważ tree zawiera już je z racji tego, że są powtórzeniami; jednakże, gdy powtarzający się podciąg kończy się napotykając nie powtarzający się znak, musimy utworzyć rozgałęzienie w tym punkcie, aby reprezentować rozbieżność od tego punktu.
Na przykład w przypadku ciągu 'ABCXABCY' (patrz poniżej), rozgałęzienie do X i Y należy dodać do trzech różnych przyrostków, ABC, BC i C ; w przeciwnym razie nie jest poprawnym drzewem sufiksów i nie możemy znaleźć wszystkich podłańcuchów łańcucha poprzez dopasowanie znaków z korzenia w dół.
Jeszcze raz, aby podkreślić – każda operacja wykonywana na sufiksie w drzewie musi być odzwierciedlona przez kolejne sufiksy (np. ABC > BC > C), w przeciwnym razie po prostu przestają być poprawnymi sufiksami.
Ale nawet jeśli zaakceptujemy, że musimy wykonać te ręczne aktualizacje, skąd wiemy, ile sufiksów musi być aktualizacja? Ponieważ, kiedy dodamy powtarzający się znak A (i resztę powtarzających się znaków po kolei), nie mamy jeszcze pojęcia, kiedy / gdzie musimy podzielić sufiks na dwie gałęzie. Konieczność podziału jest stwierdzana dopiero wtedy, gdy natkniemy się na pierwszy nie powtarzający się znak, w tym przypadku Y (zamiast X , który już istnieje w drzewie).
To, co możemy zrobić, to dopasować najdłuższy powtarzany ciąg, jaki możemy, i policzyć, ile z jego sufiksów potrzebujemy do aktualizacji później. To właśnie oznacza 'reszta' .
[[20]}pojęcie "pozostałość" i "ponowne skanowanie"Zmienna remainder mówi nam, ile powtarzających się znaków dodaliśmy w sposób niejawny, bez rozgałęzień; tzn. ile sufiksów musimy odwiedzić, aby powtórzyć operację rozgałęzienia po znalezieniu pierwszego znaku, którego nie możemy dopasować. To w zasadzie równa się temu, ile znaków "głęboko" znajdujemy się w drzewie od jego korzenia.
Tak więc, pozostając przy poprzednim przykładzie z ciągu ABCXABCY , dopasowujemy powtórzoną ABC część 'implicite', inkrementując remainder za każdym razem, co daje resztę 3. Następnie napotykamy nie powtarzający się znak ' Y ' . Tutaj dzielimy wcześniej dodany ABCX na ABC->x i ABC->Y . Następnie zmniejszamy remainder z 3 do 2, ponieważ zajęliśmy się już rozgałęzieniemABC. Teraz powtarzamy operację dopasowując ostatnie 2 znaki – BC - od korzenia do punktu, w którym musimy się podzielić, i dzielimy BCX także na BC->X i BC->Y . Ponownie zmniejszamy remainder do 1 i powtarzamy operację; aż remainder będzie równe 0. Na koniec, musimy dodać również bieżący znak ( Y ) do katalogu głównego.
Ta operacja, po kolejnych przyrostkach z korzenia, aby dotrzeć do punktu, w którym musimy wykonać operację, nazywa się 'rescanning' w algorytmie Ukkonena i zazwyczaj jest to najdroższa część algorytmu. Wyobraź sobie dłuższy ciąg znaków, w którym musisz "przeskanować" długie podłańcuchy, w wielu dziesiątkach węzłów (omówimy to później), potencjalnie tysiące razy.
Jako rozwiązanie wprowadzamy to, co nazywamy "łączami przyrostkowymi" .
Pojęcie "łącza przyrostkowe"Linki przyrostkowe w zasadzie wskazują na pozycje, które normalnie musielibyśmy 'przeskanować', więc zamiast kosztownej operacji rescan możemy po prostu przejść do pozycji połączonej, wykonać naszą pracę, przejść do następnej pozycji połączonej i powtórzyć-aż nie ma już pozycji do aktualizacji.
Oczywiście jednym dużym pytaniem jest, jak dodać te linki. Istniejącą odpowiedzią jest to, że możemy dodawać linki, gdy wstawiamy nowe węzły gałęzi, wykorzystując fakt, że w każdym rozszerzeniu drzewa, węzły gałęzi są naturalnie tworzone jeden po drugim w dokładnej kolejności, w jakiej musimy je połączyć razem. Musimy jednak połączyć się z ostatnim utworzonym węzłem gałęzi (najdłuższym sufiksem) do poprzednio utworzonego, więc musimy buforować ostatni utworzony przez nas węzeł, połączyć go z następnym utworzonym przez nas węzłem i buforować nowo utworzony.
Jedną z konsekwencji jest to, że w rzeczywistości często nie mamy linków sufiksowych do naśladowania, ponieważ dany węzeł gałęzi został właśnie utworzony. W takich przypadkach musimy jeszcze wrócić do wspomnianego 'rescanning' z roota. Dlatego po wstawieniu, jesteś poinstruowany, aby albo użyć łącza przyrostka, albo przejść do root.
(lub alternatywnie, jeśli przechowujesz wskaźniki rodzica w węzłach, możesz spróbować podążać za rodzicami, sprawdzić, czy mają łącze i użyć tego. Zauważyłem, że jest to bardzo rzadko wspominane, ale użycie łącza przyrostkowego nie jest ustawione w kamieniach. istnieje wiele możliwych podejść, a jeśli rozumiesz podstawowy mechanizm, możesz wdrożyć taki, który najlepiej pasuje do Twoich potrzeb.)
Pojęcie " aktywny punkt "
Do tej pory omawialiśmy wiele wydajnych narzędzi do budowy drzewa i niejasno nawiązaliśmy do trawersowania przez wiele krawędzi i węzłów, ale nie zbadaliśmy jeszcze odpowiednich konsekwencji i złożoności.
Wcześniej wyjaśnione pojęcie 'reszta' {[10] } jest przydatne do śledzenia, gdzie jesteśmy w drzewie, ale musimy zdać sobie sprawę, że nie przechowuje ono wystarczającej ilości informacji.
Po pierwsze, zawsze znajdujemy się na określonej krawędzi węzła, więc musimy przechowywać informacje o krawędzi. Nazywamy to 'active edge' .
Po drugie, nawet po dodaniu informacji o krawędzi, nadal nie mamy możliwości zidentyfikowania pozycji, która jest dalej w drzewie i nie jest bezpośrednio połączona z węzłemkorzenia . Więc musimy również przechowywać węzeł. Nazwijmy to 'aktywny węzeł' .
Wreszcie możemy zauważyć, że 'reszta' jest nieodpowiednia do identyfikacji pozycji na krawędzi, która nie jest bezpośrednio połączona z rootem, ponieważ 'reszta' to długość całej trasy; i prawdopodobnie nie chcemy zawracać sobie głowy zapamiętywaniem i odejmowaniem długości poprzednich krawędzi. Potrzebujemy więc reprezentacji, która jest zasadniczo pozostałością na bieżącej krawędzi . To właśnie nazywamy "aktywną długością" .
Prowadzi to do tego, co nazywamy 'active point' - pakietu trzech zmiennych, które zawierają wszystkie informacje potrzebne do utrzymania naszej pozycji w Drzewo:
Active Point = (Active Node, Active Edge, Active Length)
Możesz zaobserwować na poniższym obrazku, jak dopasowana trasa ABCABDskłada się z 2 znaków na krawędzi AB (z root), plus 4 znaki na krawędzi CABDABCABD (z węzła 4) – co daje 'pozostałość' 6 znaków. Tak więc, nasza obecna pozycja może być zidentyfikowana jako aktywny węzeł 4, aktywna krawędź C, aktywna Długość 4 .
Kolejna ważna rola 'active point' jest to, że stanowi warstwę abstrakcyjną dla naszego algorytmu, co oznacza, że części naszego algorytmu mogą wykonywać swoją pracę na 'Active point' , niezależnie od tego, czy ten aktywny punkt znajduje się w korzeniu, czy gdziekolwiek indziej. Dzięki temu w prosty i przejrzysty sposób zaimplementujemy w naszym algorytmie łącza przyrostkowe.
Różnice między przeskanowaniem a użyciem linków przyrostkowych
Teraz, najtrudniejsza część, coś – co – z mojego doświadczenia-może spowodować wiele błędów i bólów głowy, i jest słabo wyjaśnione w większości źródeł, jest różnica w przetwarzaniu przypadków łącza przyrostkowego vs przypadki rescan.Rozważ następujący przykład ciągu 'AAAABAAAAC':
Możesz zaobserwować powyżej, jak 'reszta' z 7 odpowiada całkowitej sumie znaków z roota, podczas gdy 'Długość aktywna' z 4 odpowiada sumie dopasowanych znaków z aktywnej krawędzi aktywny węzeł.
Teraz, po wykonaniu operacji rozgałęzienia w aktywnym punkcie, nasz aktywny węzeł może lub nie może zawierać łącze przyrostkowe.
Jeśli istnieje łącze przyrostkowe: , musimy tylko przetworzyć'active length'. 'Rest'jest nieistotne, ponieważ węzeł, do którego przeskakujemy przez łącze przyrostkowe, koduje już poprawną 'rest' w domyśle, po prostu przez to, że znajduje się w drzewie, w którym się znajduje.
Jeśli a link przyrostka nie występuje: musimy 'przeskanować' od zera/roota, co oznacza Przetworzenie całego przyrostka od początku. W tym celu musimy użyć całego 'reszty' jako podstawy ponownego skanowania.
Przykładowe porównanie przetwarzania z i bez łącza przyrostkowego
Zastanów się, co dzieje się w następnym kroku powyższego przykładu. Porównajmy, jak osiągnąć ten sam wynik – tj. przejście do następnego sufiksu do procesu-z i bez sufiksu link.
Using 'sufiks link'
Zauważ, że jeśli użyjemy sufiksu link, jesteśmy automatycznie "we właściwym miejscu". Co często nie jest ściśle prawdziwe ze względu na fakt, że "Długość aktywna" może być "niezgodna" z nową pozycją.
W powyższym przypadku, ponieważ 'Długość aktywna' wynosi 4, pracujemy z sufiksem ' ABAA', zaczynając od połączonego węzła 4. Ale po znalezieniu krawędzi odpowiada to pierwszemu znakowi przyrostka ('A' ), zauważamy, że nasza 'active length' przepełnia tę krawędź o 3 znaki. Przeskakujemy więc przez całą krawędź, do następnego węzła i zmniejszamy 'Długość aktywną' przez znaki, które pochłonęły skok.
Następnie, po znalezieniu następnej Krawędzi 'B', odpowiadającej zmniejszonemu przyrostkowi 'BAA ', wreszcie zauważamy, że długość krawędzi jest większa niż pozostała 'aktywna długość " z 3, co oznacza, że znaleźliśmy właściwe miejsce.
proszę zauważyć, że wygląda na to, że operacja ta zwykle nie jest określana jako "ponowne skanowanie", mimo że wydaje mi się, że jest bezpośrednim odpowiednikiem ponownego skanowania, tylko ze skróconą długością i punktem początkowym bez korzeni.
Using 'rescan'
Zauważ, że jeśli użyjemy tradycyjnej operacji "rescan" (tutaj udając, że nie mamy łącza przyrostkowego), to zaczynamy od wierzchołka drzewa, u korzenia, i musimy przeć w dół ponownie we właściwe miejsce, podążając wzdłuż całej długości obecnego przyrostka.
Długość tego przyrostka to 'reszta' , o której rozmawialiśmy wcześniej. Musimy pochłonąć całą resztę, aż osiągnie zero. Może to (i często ma) obejmować przeskakiwanie przez wiele węzłów, przy każdym skoku zmniejszając resztę o długość krawędzi, przez którą przeskoczyliśmy. W końcu dochodzimy do krawędzi to jest dłuższe niż nasza pozostała 'reszta' ; tutaj ustawiamy aktywną krawędź na daną krawędź, ustawiamy 'aktywna Długość' na pozostałą ' reszta ' i gotowe.
Należy jednak pamiętać, że rzeczywista zmienna 'Rest' musi być zachowana i zmniejszona tylko po każdym wstawieniu węzła. Więc to, co opisałem powyżej, zakładało użycie oddzielnej zmiennej inicjalizowanej na 'reszta' .
Uwagi na temat linków do sufiksów & rescans
1) zauważ, że obie metody prowadzą do tego samego wyniku. Przeskakiwanie łącza przyrostkowego jest jednak w większości przypadków znacznie szybsze; to całe uzasadnienie za łączami przyrostkowymi.
2) rzeczywiste implementacje algorytmów nie muszą się różnić. Jak wspomniałem powyżej, nawet w przypadku użycia łącza przyrostkowego, 'Długość aktywna' {[10] } często nie jest zgodna z pozycją linked, ponieważ ta gałąź drzewa może zawierać dodatkowe rozgałęzienia. Więc zasadniczo wystarczy użyć 'Active length' zamiast 'Rest' i wykonać tę samą logikę przeskanowania, aż znajdziesz krawędź krótszą niż pozostała długość przyrostka.
3) jedną z ważnych uwag dotyczących wydajności jest to, że nie ma potrzeby sprawdzania każdej postaci podczas ponownego skanowania. Ze względu na sposób budowy poprawnego drzewa sufiksów, możemy bezpiecznie założyć, że znaki pasują. Więc głównie liczysz długości, a jedyną potrzebą charakteru sprawdzanie równoważności powstaje, gdy przeskakujemy do nowej krawędzi, ponieważ krawędzie są identyfikowane przez ich pierwszy znak (który jest zawsze unikalny w kontekście danego węzła). Oznacza to, że logika 'przeskanowania' różni się od logiki dopasowywania całego łańcucha znaków (tzn. szukania fragmentu w drzewie).
4) oryginalny sufiks łączący opisany tutaj jest tylko jednym z możliwych podejść. Na przykład NJ Larsson et al. nazywa to podejście jako zorientowane na węzeł Top-Down i porównuje ją doNode-Oriented Bottom-Up i dwóchEdge-Oriented odmian. Różne podejścia mają różne typowe i najgorsze wyniki, wymagania, ograniczenia itp., ale ogólnie wydaje się, że podejście zorientowane na krawędźjest ogólną poprawą w stosunku do oryginału.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2019-04-24 09:58:09
Dzięki za dobrze wyjaśniony tutorial autorstwa @ jogojapan , zaimplementowałem algorytm w Pythonie.
Kilka drobnych problemów wymienionych przez @ jogojapan okazuje się być bardziej wyrafinowane niż się spodziewałem, i trzeba je traktować bardzo ostrożnie. Kosztowało mnie kilka dni, aby moja implementacja wystarczająco solidna (przypuszczam). Problemy i rozwiązania są wymienione poniżej:
End with
Remainder > 0okazuje się, że taka sytuacja może się również zdarzyć podczas rozwijanego kroku , a nie tylko końca całego algorytmu. Gdy tak się stanie, możemy pozostawić pozostałe znaki, actnode, actedge i actlength bez zmian, zakończyć bieżący krok rozwijania i rozpocząć kolejny krok przez składanie lub rozkładanie w zależności od tego, czy następny znak w oryginalnym łańcuchu znajduje się na bieżącej ścieżce, czy nie.-
Przeskocz nad węzłami: gdy podążamy za łączem przyrostkowym, zaktualizuj aktywny punkt, a następnie stwierdzamy, że jego active_length komponent nie działa dobrze z nowym active_node. Musimy iść do przodu we właściwe miejsce, aby podzielić, lub wstawić liść. Ten proces może być nie tak prosty ponieważ podczas przenoszenia actlength i actedge zmieniają się do końca, kiedy musisz wrócić do węzła głównego , actedge i actlength mogą być błędne z powodu tych ruchów. Potrzebujemy dodatkowej zmiennej(s), aby zachować to informacje.
Pozostałe dwa problemy zostały jakoś wskazane przez @ managonov
Dzielenie może ulegać degeneracji gdy próbujesz podzielić krawędź, czasami przekonasz się, że operacja dzielenia jest dokładnie na węźle. W tym przypadku musimy tylko dodać nowy liść do tego węzła, wziąć to jako standardową operację podziału krawędzi, co oznacza, że łącza przyrostkowe, jeśli istnieją, powinny być utrzymane / align = "left" /
Ukryte łącza przyrostkowe Istnieje inny szczególny przypadek, który wiąże się z problemem 1 i problemem 2 . Czasami musimy przeskoczyć przez kilka węzłów do właściwego punktu do podziału, możemy przekroczyć właściwy punkt, jeśli przeniesiemy się przez porównanie pozostałego ciągu znaków i etykiet ścieżki. W takim przypadku łącze przyrostkowe zostanie pominięte nieumyślnie, jeśli takie istnieje. Można tego uniknąć poprzez zapamiętanie prawa punkt w momencie przechodzenia do przodu. Łącze przyrostkowe powinno być utrzymane, jeśli węzeł split już istnieje, lub nawet problem 1 występuje podczas rozwijającego się kroku.
Na koniec moja implementacja w Pythonie wygląda następująco:
Porady: zawiera naiwną funkcję drukowania drzewa w powyższym kodzie, co jest bardzo ważne podczas debugowania . Oszczędziło mi to wiele czas i jest wygodny do lokalizowania specjalnych przypadków.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-08-02 14:38:38
@Jogojapan przyniosłeś świetne wyjaśnienie i wizualizację. Ale jak wspomniał @makagonov brakuje pewnych zasad dotyczących ustawiania linków sufiksowych. Jest widoczny w ładny sposób, gdy idziesz krok po kroku na http://brenden.github.io/ukkonen-animation / przez słowo "aabaaabb". Gdy przechodzisz od kroku 10 do kroku 11, nie ma łącza przyrostkowego od węzła 5 do węzła 2, ale aktywny punkt nagle się tam przesuwa.
@makagonov ponieważ mieszkam w świecie Javy również starałem się śledzić Twoją implementację aby uchwycić ST building workflow, ale to było dla mnie trudne z powodu:
- łączenie krawędzi z węzłami
- używanie wskaźników zamiast referencji
- łamie wypowiedzi;
- continue statements;
Więc skończyłem z taką implementacją w Javie, która mam nadzieję odzwierciedla wszystkie kroki w jaśniejszy sposób i skróci czas nauki dla innych ludzi Javy:
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class ST {
public class Node {
private final int id;
private final Map<Character, Edge> edges;
private Node slink;
public Node(final int id) {
this.id = id;
this.edges = new HashMap<>();
}
public void setSlink(final Node slink) {
this.slink = slink;
}
public Map<Character, Edge> getEdges() {
return this.edges;
}
public Node getSlink() {
return this.slink;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"id\"")
.append(":")
.append(this.id)
.append(",")
.append("\"slink\"")
.append(":")
.append(this.slink != null ? this.slink.id : null)
.append(",")
.append("\"edges\"")
.append(":")
.append(edgesToString(word))
.append("}")
.toString();
}
private StringBuilder edgesToString(final String word) {
final StringBuilder edgesStringBuilder = new StringBuilder();
edgesStringBuilder.append("{");
for(final Map.Entry<Character, Edge> entry : this.edges.entrySet()) {
edgesStringBuilder.append("\"")
.append(entry.getKey())
.append("\"")
.append(":")
.append(entry.getValue().toString(word))
.append(",");
}
if(!this.edges.isEmpty()) {
edgesStringBuilder.deleteCharAt(edgesStringBuilder.length() - 1);
}
edgesStringBuilder.append("}");
return edgesStringBuilder;
}
public boolean contains(final String word, final String suffix) {
return !suffix.isEmpty()
&& this.edges.containsKey(suffix.charAt(0))
&& this.edges.get(suffix.charAt(0)).contains(word, suffix);
}
}
public class Edge {
private final int from;
private final int to;
private final Node next;
public Edge(final int from, final int to, final Node next) {
this.from = from;
this.to = to;
this.next = next;
}
public int getFrom() {
return this.from;
}
public int getTo() {
return this.to;
}
public Node getNext() {
return this.next;
}
public int getLength() {
return this.to - this.from;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"content\"")
.append(":")
.append("\"")
.append(word.substring(this.from, this.to))
.append("\"")
.append(",")
.append("\"next\"")
.append(":")
.append(this.next != null ? this.next.toString(word) : null)
.append("}")
.toString();
}
public boolean contains(final String word, final String suffix) {
if(this.next == null) {
return word.substring(this.from, this.to).equals(suffix);
}
return suffix.startsWith(word.substring(this.from,
this.to)) && this.next.contains(word, suffix.substring(this.to - this.from));
}
}
public class ActivePoint {
private final Node activeNode;
private final Character activeEdgeFirstCharacter;
private final int activeLength;
public ActivePoint(final Node activeNode,
final Character activeEdgeFirstCharacter,
final int activeLength) {
this.activeNode = activeNode;
this.activeEdgeFirstCharacter = activeEdgeFirstCharacter;
this.activeLength = activeLength;
}
private Edge getActiveEdge() {
return this.activeNode.getEdges().get(this.activeEdgeFirstCharacter);
}
public boolean pointsToActiveNode() {
return this.activeLength == 0;
}
public boolean activeNodeIs(final Node node) {
return this.activeNode == node;
}
public boolean activeNodeHasEdgeStartingWith(final char character) {
return this.activeNode.getEdges().containsKey(character);
}
public boolean activeNodeHasSlink() {
return this.activeNode.getSlink() != null;
}
public boolean pointsToOnActiveEdge(final String word, final char character) {
return word.charAt(this.getActiveEdge().getFrom() + this.activeLength) == character;
}
public boolean pointsToTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() == this.activeLength;
}
public boolean pointsAfterTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() < this.activeLength;
}
public ActivePoint moveToEdgeStartingWithAndByOne(final char character) {
return new ActivePoint(this.activeNode, character, 1);
}
public ActivePoint moveToNextNodeOfActiveEdge() {
return new ActivePoint(this.getActiveEdge().getNext(), null, 0);
}
public ActivePoint moveToSlink() {
return new ActivePoint(this.activeNode.getSlink(),
this.activeEdgeFirstCharacter,
this.activeLength);
}
public ActivePoint moveTo(final Node node) {
return new ActivePoint(node, this.activeEdgeFirstCharacter, this.activeLength);
}
public ActivePoint moveByOneCharacter() {
return new ActivePoint(this.activeNode,
this.activeEdgeFirstCharacter,
this.activeLength + 1);
}
public ActivePoint moveToEdgeStartingWithAndByActiveLengthMinusOne(final Node node,
final char character) {
return new ActivePoint(node, character, this.activeLength - 1);
}
public ActivePoint moveToNextNodeOfActiveEdge(final String word, final int index) {
return new ActivePoint(this.getActiveEdge().getNext(),
word.charAt(index - this.activeLength + this.getActiveEdge().getLength()),
this.activeLength - this.getActiveEdge().getLength());
}
public void addEdgeToActiveNode(final char character, final Edge edge) {
this.activeNode.getEdges().put(character, edge);
}
public void splitActiveEdge(final String word,
final Node nodeToAdd,
final int index,
final char character) {
final Edge activeEdgeToSplit = this.getActiveEdge();
final Edge splittedEdge = new Edge(activeEdgeToSplit.getFrom(),
activeEdgeToSplit.getFrom() + this.activeLength,
nodeToAdd);
nodeToAdd.getEdges().put(word.charAt(activeEdgeToSplit.getFrom() + this.activeLength),
new Edge(activeEdgeToSplit.getFrom() + this.activeLength,
activeEdgeToSplit.getTo(),
activeEdgeToSplit.getNext()));
nodeToAdd.getEdges().put(character, new Edge(index, word.length(), null));
this.activeNode.getEdges().put(this.activeEdgeFirstCharacter, splittedEdge);
}
public Node setSlinkTo(final Node previouslyAddedNodeOrAddedEdgeNode,
final Node node) {
if(previouslyAddedNodeOrAddedEdgeNode != null) {
previouslyAddedNodeOrAddedEdgeNode.setSlink(node);
}
return node;
}
public Node setSlinkToActiveNode(final Node previouslyAddedNodeOrAddedEdgeNode) {
return setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, this.activeNode);
}
}
private static int idGenerator;
private final String word;
private final Node root;
private ActivePoint activePoint;
private int remainder;
public ST(final String word) {
this.word = word;
this.root = new Node(idGenerator++);
this.activePoint = new ActivePoint(this.root, null, 0);
this.remainder = 0;
build();
}
private void build() {
for(int i = 0; i < this.word.length(); i++) {
add(i, this.word.charAt(i));
}
}
private void add(final int index, final char character) {
this.remainder++;
boolean characterFoundInTheTree = false;
Node previouslyAddedNodeOrAddedEdgeNode = null;
while(!characterFoundInTheTree && this.remainder > 0) {
if(this.activePoint.pointsToActiveNode()) {
if(this.activePoint.activeNodeHasEdgeStartingWith(character)) {
activeNodeHasEdgeStartingWithCharacter(character, previouslyAddedNodeOrAddedEdgeNode);
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
rootNodeHasNotEdgeStartingWithCharacter(index, character);
}
else {
previouslyAddedNodeOrAddedEdgeNode = internalNodeHasNotEdgeStartingWithCharacter(index,
character, previouslyAddedNodeOrAddedEdgeNode);
}
}
}
else {
if(this.activePoint.pointsToOnActiveEdge(this.word, character)) {
activeEdgeHasCharacter();
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
previouslyAddedNodeOrAddedEdgeNode = edgeFromRootNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
else {
previouslyAddedNodeOrAddedEdgeNode = edgeFromInternalNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
}
}
}
}
private void activeNodeHasEdgeStartingWithCharacter(final char character,
final Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByOne(character);
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private void rootNodeHasNotEdgeStartingWithCharacter(final int index, final char character) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
this.activePoint = this.activePoint.moveTo(this.root);
this.remainder--;
assert this.remainder == 0;
}
private Node internalNodeHasNotEdgeStartingWithCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private void activeEdgeHasCharacter() {
this.activePoint = this.activePoint.moveByOneCharacter();
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private Node edgeFromRootNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByActiveLengthMinusOne(this.root,
this.word.charAt(index - this.remainder + 2));
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private Node edgeFromInternalNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private ActivePoint walkDown(final int index) {
while(!this.activePoint.pointsToActiveNode()
&& (this.activePoint.pointsToTheEndOfActiveEdge() || this.activePoint.pointsAfterTheEndOfActiveEdge())) {
if(this.activePoint.pointsAfterTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge(this.word, index);
}
else {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
return this.activePoint;
}
public String toString(final String word) {
return this.root.toString(word);
}
public boolean contains(final String suffix) {
return this.root.contains(this.word, suffix);
}
public static void main(final String[] args) {
final String[] words = {
"abcabcabc$",
"abc$",
"abcabxabcd$",
"abcabxabda$",
"abcabxad$",
"aabaaabb$",
"aababcabcd$",
"ababcabcd$",
"abccba$",
"mississipi$",
"abacabadabacabae$",
"abcabcd$",
"00132220$"
};
Arrays.stream(words).forEach(word -> {
System.out.println("Building suffix tree for word: " + word);
final ST suffixTree = new ST(word);
System.out.println("Suffix tree: " + suffixTree.toString(word));
for(int i = 0; i < word.length() - 1; i++) {
assert suffixTree.contains(word.substring(i)) : word.substring(i);
}
});
}
}
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2017-04-29 17:02:13
Moja intuicja jest następująca:
Po iteracjach k pętli głównej stworzyłeś drzewo sufiksów, które zawiera wszystkie sufiksy całego ciągu znaków, które rozpoczynają się od pierwszych znaków K.
Na początku oznacza to, że drzewo sufiksów zawiera pojedynczy węzeł korzeniowy, który reprezentuje cały ciąg znaków (jest to jedyny sufiks zaczynający się od 0).
Po iteracji len (string) masz drzewo sufiksów, które zawiera wszystkie sufiksy.
Podczas pętli klucz jest aktywny punkt. Domyślam się, że reprezentuje najgłębszy punkt w drzewie sufiksów, który odpowiada właściwemu sufiksowi pierwszych znaków K łańcucha. (Myślę, że proper oznacza, że sufiks nie może być całym ciągiem.)
Na przykład, załóżmy, że widziałeś znaki 'abcabc'. Punkt aktywny reprezentowałby punkt w drzewie odpowiadający sufiksowi "abc".
Aktywny punkt jest reprezentowany przez (origin, first, last). Oznacza to, że jesteś obecnie w wskaż w drzewie, do którego się dostajesz, zaczynając od początku węzła, a następnie wpisując znaki w łańcuchu [first:last]
Kiedy dodajesz nową postać, sprawdzasz, czy aktywny punkt nadal znajduje się w istniejącym drzewie. Jeśli tak, to jesteś skończony. W przeciwnym razie musisz dodać nowy węzeł do drzewa sufiksów w aktywnym punkcie, cofnąć się do następnego najkrótszego dopasowania i sprawdzić ponownie.
Uwaga 1: Wskaźnik sufiksu daje łącze do następnego najkrótszego dopasowania dla każdego węzła.
Uwaga 2: Po dodaniu nowego węzła i elementu zapasowego dodaje się nowy wskaźnik sufiksu dla nowego węzła. Docelowym dla tego wskaźnika przyrostka będzie węzeł w skróconym aktywnym punkcie. Ten węzeł albo już istnieje, albo zostanie utworzony w następnej iteracji tej pętli awaryjnej.
Uwaga 3: część kanonizacyjna po prostu oszczędza czas na sprawdzaniu aktywnego punktu. Załóżmy na przykład, że zawsze używałeś origin=0 i zmieniałeś tylko first I last. Aby sprawdzić aktywny punkt należy postępować zgodnie z drzewo sufiksowe za każdym razem wzdłuż wszystkich węzłów pośrednich. Sensowne jest buforowanie wyniku podążania tą ścieżką, rejestrując Tylko odległość od ostatniego węzła.
Czy możesz podać przykład kodu, co masz na myśli mówiąc" naprawić " zmienne obwiedniowe?
Ostrzeżenie zdrowotne: również uważam, że ten algorytm jest szczególnie trudny do zrozumienia, więc proszę zdać sobie sprawę, że ta intuicja może być nieprawidłowa we wszystkich ważnych szczegółach...
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2012-02-26 20:41:19
Witam Próbowałem zaimplementować powyższą implementację w Rubim, proszę to sprawdzić. wygląda na to, że działa dobrze.
Jedyną różnicą w implementacji jest to, że próbowałem użyć obiektu edge zamiast używać tylko symboli.
Występuje również w https://gist.github.com/suchitpuri/9304856
require 'pry'
class Edge
attr_accessor :data , :edges , :suffix_link
def initialize data
@data = data
@edges = []
@suffix_link = nil
end
def find_edge element
self.edges.each do |edge|
return edge if edge.data.start_with? element
end
return nil
end
end
class SuffixTrees
attr_accessor :root , :active_point , :remainder , :pending_prefixes , :last_split_edge , :remainder
def initialize
@root = Edge.new nil
@active_point = { active_node: @root , active_edge: nil , active_length: 0}
@remainder = 0
@pending_prefixes = []
@last_split_edge = nil
@remainder = 1
end
def build string
string.split("").each_with_index do |element , index|
add_to_edges @root , element
update_pending_prefix element
add_pending_elements_to_tree element
active_length = @active_point[:active_length]
# if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data[0..active_length-1] == @active_point[:active_edge].data[active_length..@active_point[:active_edge].data.length-1])
# @active_point[:active_edge].data = @active_point[:active_edge].data[0..active_length-1]
# @active_point[:active_edge].edges << Edge.new(@active_point[:active_edge].data)
# end
if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data.length == @active_point[:active_length] )
@active_point[:active_node] = @active_point[:active_edge]
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0])
@active_point[:active_length] = 0
end
end
end
def add_pending_elements_to_tree element
to_be_deleted = []
update_active_length = false
# binding.pry
if( @active_point[:active_node].find_edge(element[0]) != nil)
@active_point[:active_length] = @active_point[:active_length] + 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0]) if @active_point[:active_edge] == nil
@remainder = @remainder + 1
return
end
@pending_prefixes.each_with_index do |pending_prefix , index|
# binding.pry
if @active_point[:active_edge] == nil and @active_point[:active_node].find_edge(element[0]) == nil
@active_point[:active_node].edges << Edge.new(element)
else
@active_point[:active_edge] = node.find_edge(element[0]) if @active_point[:active_edge] == nil
data = @active_point[:active_edge].data
data = data.split("")
location = @active_point[:active_length]
# binding.pry
if(data[0..location].join == pending_prefix or @active_point[:active_node].find_edge(element) != nil )
else #tree split
split_edge data , index , element
end
end
end
end
def update_pending_prefix element
if @active_point[:active_edge] == nil
@pending_prefixes = [element]
return
end
@pending_prefixes = []
length = @active_point[:active_edge].data.length
data = @active_point[:active_edge].data
@remainder.times do |ctr|
@pending_prefixes << data[-(ctr+1)..data.length-1]
end
@pending_prefixes.reverse!
end
def split_edge data , index , element
location = @active_point[:active_length]
old_edges = []
internal_node = (@active_point[:active_edge].edges != nil)
if (internal_node)
old_edges = @active_point[:active_edge].edges
@active_point[:active_edge].edges = []
end
@active_point[:active_edge].data = data[0..location-1].join
@active_point[:active_edge].edges << Edge.new(data[location..data.size].join)
if internal_node
@active_point[:active_edge].edges << Edge.new(element)
else
@active_point[:active_edge].edges << Edge.new(data.last)
end
if internal_node
@active_point[:active_edge].edges[0].edges = old_edges
end
#setup the suffix link
if @last_split_edge != nil and @last_split_edge.data.end_with?@active_point[:active_edge].data
@last_split_edge.suffix_link = @active_point[:active_edge]
end
@last_split_edge = @active_point[:active_edge]
update_active_point index
end
def update_active_point index
if(@active_point[:active_node] == @root)
@active_point[:active_length] = @active_point[:active_length] - 1
@remainder = @remainder - 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(@pending_prefixes.first[index+1])
else
if @active_point[:active_node].suffix_link != nil
@active_point[:active_node] = @active_point[:active_node].suffix_link
else
@active_point[:active_node] = @root
end
@active_point[:active_edge] = @active_point[:active_node].find_edge(@active_point[:active_edge].data[0])
@remainder = @remainder - 1
end
end
def add_to_edges root , element
return if root == nil
root.data = root.data + element if(root.data and root.edges.size == 0)
root.edges.each do |edge|
add_to_edges edge , element
end
end
end
suffix_tree = SuffixTrees.new
suffix_tree.build("abcabxabcd")
binding.pry
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/doraprojects.net/template/agent.layouts/content.php on line 54
2014-03-03 03:32:44




